Proprietà che legano moltiplicazioni e divisioni

La moltiplicazione e la divisione sono due operazioni chiamate operazioni inverse, cioè per “tornare indietro” dopo aver fatto una moltiplicazione bisogna fare una divisione e viceversa, detto questo vediamo la tecnica per fare questo passaggio.

Fin dalle scuole elementari sappiamo che la divisione è definita tramite la moltiplicazione nel seguente modo

$6:2=3 \:perchè\: 3\cdot 2=6$

oppure scritta nello schema generale

$a:b=c \:perchè\: c\cdot b=a$

Vediamo che questa semplice proprietà risulta evidente tramite un disegno

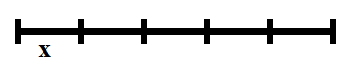
se il singolo pezzettino ( $x$ ) si ottiene dividendo in parti uguali (in questo caso 5) il segmento di partenza, allora ripetendo (cioè moltiplicando) il singolo pezzettino ( $x$ ) per lo stesso numero di volte (5) si riottiene il segmento di partenza.

Vediamo che questa proprietà risulta particolarmente utile per risolvere problemi del tipo:

Che numero deve stare al posto della $x$ se: $x\cdot 6=42$
Che numero deve stare al posto della $x$ se: $6\cdot x=42$

Che numero deve stare al posto della $x$ se: $x:6=12$
Che numero deve stare al posto della $x$ se: $48:x=12$

Vediamo come affrontare questi problemi con questa relazione.

Caso 1/2

I primi due casi, $x\cdot6$ e $6\cdot x$ , sono esattamente lo stesso caso, questo a livello teorico segue dalla proprietà commutativa della moltiplicazione che ci dice che invertendo l’ordine dei fattori il prodotto non cambia, pertanto li analizzeremo come unico caso.

La domanda, posta in italiano, consiste nel capire per che numero bisogna moltiplicare 6 per ottenere 42, quindi risulta chiaro dalla proprietà vista prima (attenzione che la proprietà è letta al contrario cioè da destra a sinistra) che

$6\cdot x =42 \:allora\: x=42:6$

ATTENZIONE: questa numero può anche essere trovato facendo la tabellina del 6 fino a giungere al numero 42, ciò non toglie che l’operazione che concettualmente abbiamo risolto sia una divisione e NON una moltiplicazione

Infatti facendo un disegno risulta chiaro

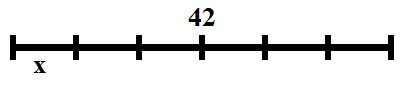
se il segmento nero (42) lo abbiamo ottenuto ripetendo 6 volte il pezzettino ( $x$ ) allora il segmento nero è diviso in 6 parti uguali ognuna grande quanto il pezzettino $x$ , cioè $x$ è il risultato della divisione.

Caso 3

Il caso 3, cioè $x:6=12$ , utilizza esattamente la proprietà vista sopra, infatti

$x:6=12 \:perchè\: 6\cdot 12=x$

Ancora una volta un disegno è assolutamente chiarificatore

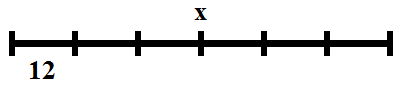
se dividendo il segmento nero ( $x$ ) in 6 parti uguali otteniamo come risultato 12 (singolo pezzettino) allora il segmento grande lo possiamo ottenere ripetendo (cioè moltiplicando) il numero 12 per 6 volte.

Caso 4

Vediamo infine il caso 4, ossia $48:x=12$ , e anche qui utilizziamo esattamente la proprietà vista precedentemente, infatti

$48:x=12 \:perchè\: 12\cdot x=48 \:da\; cui\; usando\; il\; caso\; 1/2\: x=48:12$

Anche qui vediamo di spiegare il tutto attraverso un disegno

se il segmento nero (48) viene diviso in un numero di parti ignoto ( $x$ ) e come risultato ottengo 12, allora devo trovare quante volte devo ripetere il 12 per ottenere 48 come risultato, cioè devo risolvere la divisione 48:12, cioè capire quante volte il 12 entra dentro il 48.

Dopo questa lezione vediamo di consolidare i concetti con una serie di esercizi mirati. Vai ai quiz (il quiz verrà aperto in una nuova scheda):

Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9

Brevi lezioni

Proprietà che legano moltiplicazioni e divisioni

Lascia un commento Annulla risposta