Esercizio 75 sui vettori e le forze – Esercizi svolti – FISICA

Le tre forze nella figura hanno intensità $F_1=F_2=F$ , $F_3=2F$

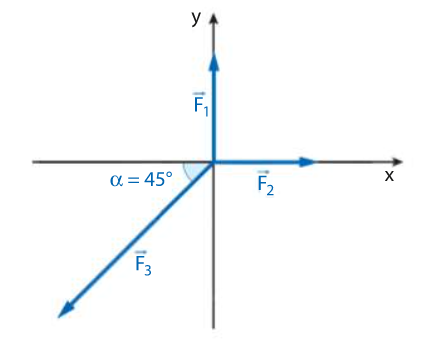
Determina modulo, direzione e verso della risultante.

SVOLGIMENTO

Sappiamo che la forza risultante è per definizione la somma vettoriale delle forze in gioco, pertanto

$\vec{F}_{tot}=\vec{F}_1+\vec{F}_2+\vec{F}_3$

Risolviamo questo esercizio in due maniere diverse.
Nel primo modo determiniamo le tre forze presenti nell’esercizio in componenti cartesiane e poi andiamo a calcolare le componenti cartesiane della risultante. Quindi

$\vec{F}_1=(0\: N\:;\: F)$

$\vec{F}_2=(F\:;\: 0\: N)$

$\vec{F}_3=2F\cdot (\cos{225^\circ}\:;\: \sin{225^\circ})$

da cui

$\vec{F}_{tot}=F\cdot ((0\:;\: 1)+(1\:;\: 0)+(2\cdot \cos{225^\circ}\:;\: 2\cdot \sin{225^\circ}))$

$\vec{F}_{tot}=F\cdot (1-{2\over \sqrt{2}}\:;\: 1-{2\over \sqrt{2}})=F\cdot (1- \sqrt{2}\:;\: 1-\sqrt{2})$

Una volta fatto questo possiamo facilmente capire che il vettore risultante è diretto come $\vec{F}_3$ , infatti le sue due componenti sono uguali e negative entrambe, inoltre il modulo lo possiamo calcolare con il teorema di Pitagora, pertanto

$F_{tot}=F\cdot \sqrt{(1-\sqrt{2})^2+(1-\sqrt{2})^2}=F\cdot \sqrt{2\cdot (1-\sqrt{2})^2}$

$F_{tot}=F\cdot\sqrt{2}\cdot \sqrt{(1-\sqrt{2})^2}=F\cdot\sqrt{2}\cdot \left|(1-\sqrt{2})\right|=F\cdot (2-\sqrt{2})$

La seconda tecnica per arrivare allo stesso risultato è lavorare con furbizia sulle simmetrie della figura, infatti da

$\vec{F}_{tot}=\vec{F}_1+\vec{F}_2+\vec{F}_3$

facendo prima la somma $\vec{F}_1+\vec{F}_2$ otteniamo facilmente che questa somma è il vettore

$(F\:;\: F)$

di modulo

$\sqrt{F^2+F^2}=F\cdot \sqrt{2}$

di direzione uguale a quella di $\vec{F}_3$ e di verso opposto. Pertanto per completare la somma tra i tre vettori ci basta fare la somma di due vettori con uguale direzione e verso opposto. Pertanto il verso della risultante sarà quello di $\vec{F}_3$ perchè il suo modulo, cioè $2F$ , è maggiore del modulo della somma $\vec{F}_1+\vec{F}_2$ , e il modulo sarà

$F_{tot}=F_3-(F_1+F_2)=F\cdot 2-F\cdot \sqrt{2}=F\cdot (2-\sqrt{2})$

Visualizza la soluzione

2 commenti su “Esercizio 75 sui vettori e le forze – Esercizi svolti – FISICA”

Alberto ha detto:

Gennaio 28, 2024 alle 12:29 pm

perché la direzione è la stessa ??

Rispondi
1. admin ha detto:
  
  Gennaio 28, 2024 alle 6:30 pm
  
  Immagino che la domanda sia perchè la direzione della risultante tra F1 e F2 è la stessa di F3. La risultante tra F1 e F2 è sostanzialmente la diagonale del quadrato che ha per lato F1 e F2 pertanto è diretta come la bisettrice del primo e terzo quadrante, ossia la direzione di F3.
  
  Rispondi

Brevi lezioni

Esercizio 75 sui vettori e le forze – Esercizi svolti – FISICA

SVOLGIMENTO

2 commenti su “Esercizio 75 sui vettori e le forze – Esercizi svolti – FISICA”

Rispondi a admin Annulla risposta