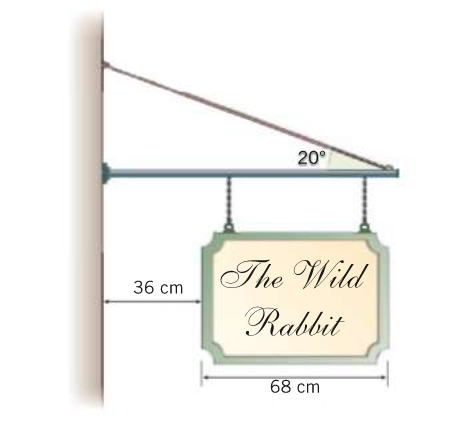
La figura mostra l’insegna di un pub. La massa dell’asta è 
e quella dell’insegna è 
. In entrambi gli oggetti le masse sono distribuite uniformemente. Calcola la tensione del cavo che regge l’estremità dell’asta.
SVOLGIMENTO
Sappiamo che siamo in una situazione di equilibrio, questo fisicamente si traduce nel fatto che la risultante delle forze e la risultante dei momenti, calcolati rispetto al punto di contatto tra asta e muro, sarà nulla. Pertanto, concentrandoci sui momenti, abbiamo che
![\[M_{asta}+M_{insegna}=M_{fune}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6b7c1fa2dcf87d0ec29a48e671ec8f0f_l3.png "Rendered by QuickLaTeX.com")
dove quest’uguaglianza in modulo dipende dal diverso segno dei vettori momenti. Da cui
![\[F_{asta}\cdot b_{asta}+F_{insegna}\cdot b_{insegna}=T\cdot b_{fune}\cdot \sin{20^\circ}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d826e67e574b0fd64152c99f2f895e5e_l3.png "Rendered by QuickLaTeX.com")
![\[0,750\: kg\cdot 9,81\: N/kg\cdot 0,52\: m+2,4\: kg\cdot 9,81\: N/kg\cdot 0,70\: m=T\cdot 1,04\: m\cdot \sin{20^\circ}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8780cb5659ff1d6f577deadbbd1717d0_l3.png "Rendered by QuickLaTeX.com")
Osserviamo esplicitamente che per calcolare i bracci si utilizza l’informazione dell’omogeneità sia dell’asta che dell’insegna, quindi consideriamo la forza peso applicata nel loro baricentro.
![\[T={0,750\: kg\cdot 9,81\: N/kg\cdot 0,52\: m+2,4\: kg\cdot 9,81\: N/kg\cdot 0,70\: m\over 1,04\: m\cdot \sin{20^\circ}}\approx 57\: N\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-0f5f48b0ee67f84da25c85efc7db00ec_l3.png "Rendered by QuickLaTeX.com")
 | TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SULL’EQUILIBRIO DEI SOLIDI |  |
dove ha preso il dato 0,52m e il 0,70m ?????????????????????????????????????????’
Buongiorno, l’asta e l’insegna hanno la loro forza peso applicata nel loro baricentro (modelizzazione che ci permette di determinare il momento della forza peso). Il baricentro lo calcoliamo utilizzando il punto medio dell’asta e il punto medio dell’insegna.
0,52m e 0,70m sono i baricentri rispettivamente dell’asta e del cartello.
Infatti il baricentro si trova nel punto medio dell’oggetto (semplificando: a metà).
Il baricentro del palo sarà a metà quindi della sua lunghezza: sommiamo la lunghezza del cartello e della distanza di esso dal muro e così otteniamo la lunghezza complessiva del palo (0,68m + 0,36m= 1,04m). A questo punto, quindi, dividiamo a metà la lunghezza del palo per individuare il baricentro (1,04m : 2 =0,52m).
Simile procedimento anche per il baricentro del cartello: il suo baricentro sarà alla metà della lunghezza di esso; dobbiamo quindi dividere a metà la lunghezza del cartello ed a quel punto sommarci la distanza dal muro (perchè il cartello e quindi anche il suo baricentro non sono adesi al muro, ma sono spostati): quindi (0,68m : 2 + 0,36m)= 0,70m.
Spero di essere stato chiaro e utile. 🙂