Un blocco di legno di massa ![]() si trova su un tavolo e viene spinto orizzontalmente.
si trova su un tavolo e viene spinto orizzontalmente.
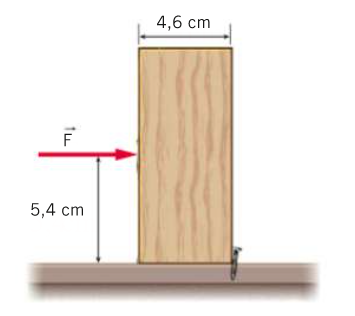
Il moto del blocco è ostacolato da un chiodo. Supponi che il blocco sia spinto da una forza di modulo ![]() e calcola il modulo della forza di reazione vincolare del tavolo sul blocco. Il blocco si muove? Supponi che il blocco sia spinto da una forza di
e calcola il modulo della forza di reazione vincolare del tavolo sul blocco. Il blocco si muove? Supponi che il blocco sia spinto da una forza di ![]() . Il blocco si muove?
. Il blocco si muove?
SVOLGIMENTO
Ipoteticamente sul blocco agiscono quattro forze: la forza peso, la forza ![]() , la reazione vincolare del chiodo e la reazione vincolare del pavimento. Rispetto all’ipotetico punto di rotazione attorno al chiodo la forza peso e la forza
, la reazione vincolare del chiodo e la reazione vincolare del pavimento. Rispetto all’ipotetico punto di rotazione attorno al chiodo la forza peso e la forza ![]() svilupperanno pertanto un momento di segno opposto, siccome tenderanno a far ruotare il blocco in due direzioni opposte, calcoliamo pertanto chi “vince” tra questi due momenti (lasciamo un attimo in sospeso il momento della reazione vincolare del pavimento):
svilupperanno pertanto un momento di segno opposto, siccome tenderanno a far ruotare il blocco in due direzioni opposte, calcoliamo pertanto chi “vince” tra questi due momenti (lasciamo un attimo in sospeso il momento della reazione vincolare del pavimento):
![]()
![]()
Quindi il momento della forza peso è maggiore del momento della forza ![]() , ma siccome il blocco non può ruotare in senso antiorario per via del vincolo del pavimento vuol dire che c’è una reazione vincolare
, ma siccome il blocco non può ruotare in senso antiorario per via del vincolo del pavimento vuol dire che c’è una reazione vincolare ![]() generata dal pavimento e diretta verso l’alto che determina un momento di modulo uguale a
generata dal pavimento e diretta verso l’alto che determina un momento di modulo uguale a ![]() , quindi
, quindi
![]()
ossia
![]()
Osserviamo anche esplicitamente che questa forza non è sufficiente a far muovere il blocco di legno.
Rispondiamo ora alla seconda parte della domanda, per avere una rotazione del blocco di legno necessitiamo che il momento generato dalla forza ![]() sia superiore del momento generato dalla forza peso, se
sia superiore del momento generato dalla forza peso, se ![]() abbiamo
abbiamo
![]()
quindi ampiamente sufficiente a contrastare il momento generato dalla forza peso.
 | TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SULL’EQUILIBRIO DEI SOLIDI |  |
Perché 0,023m e non 0,046m?
Buongiorno, la forza peso di un oggetto è applicata al suo baricentro. Il baricentro di un rettangolo omogeneo si trova nel punto di incontro delle sue diagonali, ossia nel punto che sta esattamente a metà del rettangolo. Ecco perchè si utilizza la metà della larghezza e non tutta la larghezza.