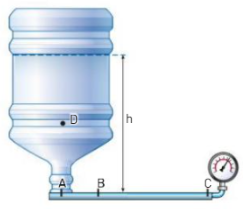
Esercizio 46 sull’equilibrio dei fluidi – Esercizi svolti – FISICA

Un boccione d’acqua è collegato tramite un sottile tubo cilindrico al rubinetto del distributore d’acqua. Eventualmente al posto del rubinetto si può collegare un manometro. Il livello dell’acqua si trova all’altezza $h=50\: cm$ dal tubo, come mostrato nella figura.

Calcola la pressione dell’acqua nei punti $A$ , $B$ e $C$ del tubo dovuta alla forza peso dell’acqua.
Come cambiano i valori se il livello dell’acqua scende fino al punto $D$ situato a un’altezza pari a $h/2$ ?

Il boccione viene poi sostituito con uno nuovo più piccolo. Collegando il manometro si misura una pressione dell’acqua di $6500\: Pa$ . Quale è il livello dell’acqua nel nuovo boccione?

SVOLGIMENTO

Innanzitutto osserviamo che, dalla legge di Stevino, si evince in maniera chiara che la differenza di pressione all’interno di un fluido è dovuta esclusivamente alla differenza di altezza all’interno del fluido stesso, pertanto nel punto $A$ , $B$ e $C$ la pressione sarà uguale. Inoltre la legge di Stevino ci dice che tale pressione sarà

$p_2=p_1+d\cdot h\cdot g$

osserviamo che in questo particolare esercizio la pressione $p_1$ , ossia la pressione a livello $h=0\: m$ , è nulla perchè il bottiglione di acqua è chiuso sopra e ci viene detto esplicitamente che la pressione nei punti $A$ , $B$ e $C$ è dovuta alla forza peso dell’acqua, quindi

$p_{A,B,C}=d\cdot h\cdot g=1000\: kg/m^3\cdot 0,5\: m\cdot 9,81\: N/kg= 4905\: Pa$

Notiamo che la formula presenta una proporzionalità diretta tra $p$ e $h$ , ne segue che quando il livello dell’acqua scende alla quota $D=h/2$ si avrà anche un dimezzamento della pressione, che quindi sarà