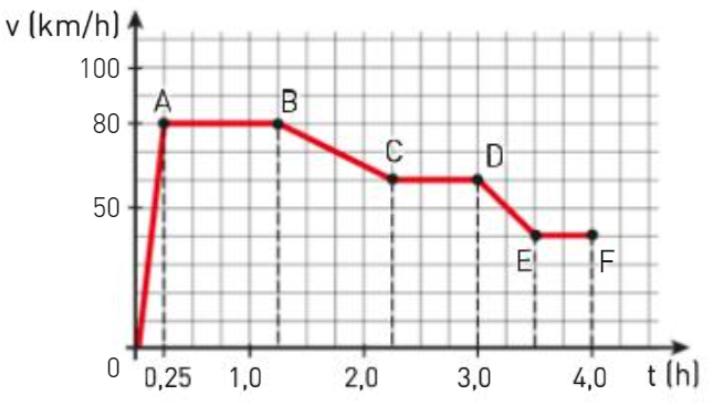
In un viaggio su un tratto rettilineo un’auto si muove secondo il seguente grafico velocità-tempo
Prima di procedere con la risoluzione dell’esercizio ricordiamo come si leggono i grafici velocità-tempo e la definizione di accelerazione media. L’accelerazione è definita come la variazione di velocità fratto il tempo necessario per ottenere tale variazione. Ossia
![Rendered by QuickLaTeX.com \[a_m={\Delta v\over \Delta t}={v_f-v_i\over t_f-t_i}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8e1135f16f33bb6063c595d07a2a1caa_l3.png)
Anche utilizzando tale definizione possiamo capire come leggere i grafici velocità-tempo: in tali grafici le parti del grafico crescenti rappresentano un moto ad accelerazione positiva, i tratti del grafico stazionari (cioè “paralleli” all’asse
) rappresentano moti ad accelerazione nulla, infine i tratti del grafico decrescenti rappresentano un moto ad accelerazione negativa. Una volta ricordato questo possiamo procedere con la risoluzione dell’esercizio. La prima cosa a cui dobbiamo fare attenzione è che questo grafico velocità-tempo ha come unità di misura i
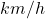
per le velocità e le
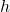
per i tempi, questo non mi darà problemi quando dovrò descrivere il moto, però nel calcolo delle accelerazioni dovrò fare attenzione a convertire tutto nelle unità di misura del sistema internazionale, altrimenti le accelerazioni mi verranno fuori in
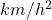
. Partiamo con la descrizione del moto.
L’automobile tra
e
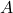
si muove con una grande accelerazione costante (grafico non solo crescente, ma anche rettilineo e molto pendente) e questo è il tratto con l’accelerazione maggiore. In seguito tra i punti
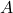
e
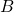
si muove a velocità costante, quindi accelerazione nulla, pari a
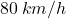
. Dopo, tra
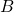
e
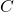
, abbiamo un tratto di decelerazione seguito, nel tratto tra
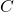
e
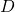
, da uno a velocità costante pari a
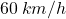
. Infine abbiamo gli ultimi due tratti: il primo tra
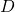
ed
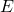
, è quello con decelerazione massima (in quanto il grafico è decrescente e rispetto all’altro pezzo decrescente ha una pendenza di “intensità” maggiore) e l’ultimo, tra
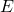
e
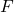
, di velocità costante uguale a
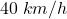
.
Calcoliamo ora le accelerazioni in ogni singolo tratto ricordando ancora una volta che le unità di misura vanno convertite in
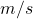
e

.
![Rendered by QuickLaTeX.com \[a_{0-A}={v_A-v_0\over t_A-t_0}\approx {22,2\: m/s-0\: m/s\over 900\:s-0\:s }\approx 0,025\: m/s^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-edcfa808d4fcf4b3750b8b19f4fc3dd7_l3.png)
![Rendered by QuickLaTeX.com \[a_{A-B}={v_B-v_A\over t_B-t_A}\approx {22,2\: m/s-22,2\: m/s\over 4500\:s-900\:s }=0\: m/s^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-63fad11e8da627ce2ea6493c1b126a4d_l3.png)
![Rendered by QuickLaTeX.com \[a_{B-C}={v_C-v_B\over t_C-t_B}\approx {16,7\: m/s-22,2\: m/s\over 8100\:s-4500\:s }\approx -1,5\cdot 10^{-3}\: m/s^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-b9bc4c5294b252fa6448a4050954a9cc_l3.png)
![Rendered by QuickLaTeX.com \[a_{C-D}={v_D-v_C\over t_D-t_C}\approx {16,7\: m/s-16,7\: m/s\over 10800\:s-8100\:s }=0\: m/s^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-5b8b52062a2d0f8cfadcaefaacdc889a_l3.png)
![Rendered by QuickLaTeX.com \[a_{D-E}={v_E-v_D\over t_E-t_D}\approx {11,1\: m/s-16,7\: m/s\over 12600\:s-10800\:s }\approx -3\cdot 10^{-3}\: m/s^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-2400bceed85601d906cd500ab1123d1b_l3.png)
![Rendered by QuickLaTeX.com \[a_{E-F}={v_F-v_E\over t_F-t_E}\approx {11,1\: m/s-11,1\: m/s\over 14400\:s-12600\:s }=0\: m/s^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-bbf773057b0f88c62ead8c43385d4d16_l3.png)
Per concludere calcoliamo l’accelerazione su tutto il tratto di tempo studiato
![Rendered by QuickLaTeX.com \[a_{0-E}={v_E-v_0\over t_E-t_0}\approx {11,1\: m/s-0\: m/s\over 14400\:s-0\:s }\approx 7,7\cdot 10^{-4}\: m/s^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-141d50221b492998492f176270729101_l3.png)