La figura mostra i vettori ![]() e
e ![]() . Il lato di ogni quadratino vale
. Il lato di ogni quadratino vale ![]() .
.
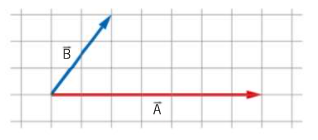
Calcola il modulo del prodotto vettoriale ![]() . Quale è il verso del vettore
. Quale è il verso del vettore ![]() ?
?
SVOLGIMENTO
Il prodotto vettoriale tra due vettori è un vettore del quale verso e direzione sono facili da determinare utilizzando la regola della “mano destra”, per quanto invece riguarda il modulo sappiamo che tale modulo si ricava con la formula
![]()
Dove ![]() è l’angolo compreso tra il vettore
è l’angolo compreso tra il vettore ![]() e il vettore
e il vettore ![]() . Siccome conosciamo i moduli dei due vettori l’unica incognita dell’esercizio sarà quindi
. Siccome conosciamo i moduli dei due vettori l’unica incognita dell’esercizio sarà quindi ![]() , vediamo come possiamo calcolarlo. Usando le formule trigonometriche sul triangolo rettangolo che ha come ipotenusa il vettore
, vediamo come possiamo calcolarlo. Usando le formule trigonometriche sul triangolo rettangolo che ha come ipotenusa il vettore ![]() e come cateti due quadratini (lungo il vettore rosso
e come cateti due quadratini (lungo il vettore rosso ![]() ) e tre quadratini verticalmente dalla punta del vettore
) e tre quadratini verticalmente dalla punta del vettore ![]() fino al vettore
fino al vettore ![]() , possiamo scrivere che
, possiamo scrivere che
![]()
da cui
![]()
per cui
![]()
Per determinare il verso attraverso la regola della mano destra bisogna, utilizzando la mano destra, sovrapporre il pollice al vettore ![]() e l’indice al vettore
e l’indice al vettore ![]() , ricordiamo esplicitamente che il prodotto vettoriale non è commutativo, il verso del prodotto vettoriale è il verso del dito medio. Pertanto in questo esercizio il prodotto vettoriale sarà perpendicolare ai vettori
, ricordiamo esplicitamente che il prodotto vettoriale non è commutativo, il verso del prodotto vettoriale è il verso del dito medio. Pertanto in questo esercizio il prodotto vettoriale sarà perpendicolare ai vettori ![]() e
e ![]() , come sempre, ed “uscirà” dal foglio.
, come sempre, ed “uscirà” dal foglio.
 | TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUI VETTORI E LE FORZE |  |