Su una molla è stato evidenziato, a riposo, il punto ![]() centrale. Quando la molla è tirata con una forza
centrale. Quando la molla è tirata con una forza ![]() , si allunga di
, si allunga di ![]() . Quanto si allungano le due parti della molla ai lati del punto centrale? A quale forza è sottoposta ciascuna di esse?
. Quanto si allungano le due parti della molla ai lati del punto centrale? A quale forza è sottoposta ciascuna di esse?
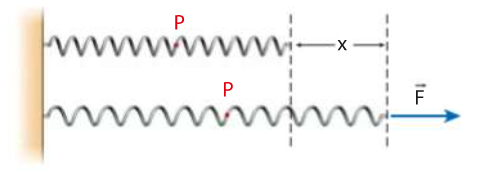
Tagliamo ora la molla in due parti uguali, in modo da ottenere due molle identiche, a ciascuna delle quali applichiamo la stessa forza ![]() . Spiega perchè le due molle hanno costante elastica doppia rispetto alla molla iniziale.
. Spiega perchè le due molle hanno costante elastica doppia rispetto alla molla iniziale.
SVOLGIMENTO
Il punto ![]() che si trova esattamente a metà della molla prima che la molla venga tirata si troverà ancora a metà della molla quando questa viene tirata, pertanto sia a destra che a sinistra di tale punto la molla si sarà allungata nello stesso modo, ossia di un valore pari a
che si trova esattamente a metà della molla prima che la molla venga tirata si troverà ancora a metà della molla quando questa viene tirata, pertanto sia a destra che a sinistra di tale punto la molla si sarà allungata nello stesso modo, ossia di un valore pari a ![]() . Inoltre la molla “trasporta” la forza
. Inoltre la molla “trasporta” la forza ![]() , cioè in ogni punto della molla sarà applicata una forza uguale alla forza
, cioè in ogni punto della molla sarà applicata una forza uguale alla forza ![]() fino al punto in cui la molla è attaccata al muro, e anche in quel punto la molla eserciterà sul muro una forza uguale a
fino al punto in cui la molla è attaccata al muro, e anche in quel punto la molla eserciterà sul muro una forza uguale a ![]() .
.
Osserviamo ora che tagliare la molla a metà è praticamente uguale a considerare metà molla solamente, infatti se noi non tagliassimo la molla ma considerassimo la molla dal muro fino al punto ![]() allora vedremmo che nel punto
allora vedremmo che nel punto ![]() è applicata una forza
è applicata una forza ![]() che fa allungare la molla di un valore pari a
che fa allungare la molla di un valore pari a ![]() , ossia metà molla è una molla di costante elastica pari al doppio della costante elastica della molla intera. Osserviamo che questo risultato non deve stupire, la costante elastica rappresenta quanta forza ci vuole per allungare una molla di un metro, è normale che più la molla è lunga e più sarà facile allungarla (a parità di caratteristiche fisiche della molla).
, ossia metà molla è una molla di costante elastica pari al doppio della costante elastica della molla intera. Osserviamo che questo risultato non deve stupire, la costante elastica rappresenta quanta forza ci vuole per allungare una molla di un metro, è normale che più la molla è lunga e più sarà facile allungarla (a parità di caratteristiche fisiche della molla).
 | TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUI VETTORI E LE FORZE |  |
esercizi sui vettori
fisicamente