Esercizi di fisica, Vettori e forze

Esercizio 1 sui vettori e le forze – Esercizi svolti – FISICA

11 commenti

I vettori \vec{A} e \vec{B} in figura hanno modulo A=1,6 e B=2,4.

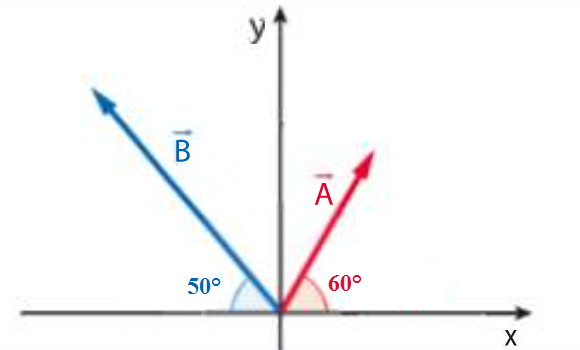
Determina il modulo del vettore somma \vec{A}+\vec{B} e l’angolo che forma con l’asse x.

SVOLGIMENTO

Per risolvere questo esercizio scegliamo di scrivere i vettori presenti nell’esercizio in coordinate cartesiane, ricordando che

    \[\vec{V}=V\cdot (\cos{\widehat{Vx}}\:;\: \sin{\widehat{Vx}})\]

pertanto

    \[\vec{A}=1,6\cdot (\cos{60^\circ}\:;\: \sin{60^\circ})\]

    \[\vec{B}=2,4\cdot (\cos{130^\circ}\:;\: \sin{130^\circ})\]

da cui

    \[\vec{A}+\vec{B}=1,6\cdot (\cos{60^\circ}\:;\: \sin{60^\circ})+2,4\cdot (\cos{130^\circ}\:;\: \sin{130^\circ})\]

    \[\vec{A}+\vec{B}\approx(0,8\:;\: 1,39)+(-1,54\:;\: 1,84)\]

    \[\vec{A}+\vec{B}=(0,8-1,54\:;\: 1,39+1,84)\]

    \[\vec{A}+\vec{B}=(-0,74\:;\:3,23)\]

Per cui il modulo lo possiamo calcolare con il teorema di Pitagora e otteniamo

    \[\left| \vec{A}+\vec{B}\right|=\sqrt{(-0,74)^2+3,23^2}\approx 3,3\]

Mentre per calcolare l’angolo possiamo utilizzare \cos^{-1}, \sin^{-1} oppure \tan^{-1}. Scegliamo di fare questo con il primo e il terzo modo, quindi

    \[(\vec{A}+\vec{B})_x=\left| \vec{A}+\vec{B}\right|\cdot \cos{\widehat{Ax}}\Rightarrow \cos{\widehat{Ax}}={(\vec{A}+\vec{B})_x\over \left| \vec{A}+\vec{B}\right|}\]

da cui

    \[\widehat{Ax}=\cos^{-1}{(\vec{A}+\vec{B})_x\over \left| \vec{A}+\vec{B}\right|}=\cos^{-1}{-0,74\over 3,3}\approx 103^\circ\]

mentre usando l’arcotangente (o \tan^{-1}) verrebbe

    \[\widehat{Ax}=\arctan{{(\vec{A}+\vec{B})_y\over (\vec{A}+\vec{B})_x}}=\arctan{{3,23\over -0,74}}\approx 103^\circ\]

Visualizza la soluzione

TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUI VETTORI E LE FORZE


11 commenti su “Esercizio 1 sui vettori e le forze – Esercizi svolti – FISICA”

    1. Il modulo dei vettori non è mai negativo. In fisica (e più raramente in matematica) si utilizzano i vettori di modulo negativo per indicare che il vettore è di verso contrario a un verso che universalmente consideriamo positivo, ad esempio il vettore accelerazione di gravità generalmente viene considerato negativo perchè diretto verso la Terra mentre l’asse y è diretta verso l’alto.

      Rispondi

    1. Perchè gli angoli si misurano a partire dall’asse x, che è l’angolo 0°, in senso antiorario. Quindi per calcolare l’angolo devi fare 180°-50°. Se tu usassi l’angolo di 50° la coordinata x del vettore ti verrebbe positiva, in valore assoluto corretta, però con il segno sbagliato.

      Rispondi

    2. perché l’angolo del vettore B parte dallo stesso punto di quello del vettore A, quindi sottraendo 50 (dato che ci forniscono) a 180 (angolo piatto) ci esce 130

      Rispondi

    1. Buonasera, se calcoli l’arcotangente il risultato è -77° che equivale a un angolo di 103° contando che la funzione è periodica di periodo Pi greco.

      Rispondi

  5. Grazie mille!! Ottimo sito per gli esercizi e soprattutto per le soluzioni con spiegazione, complimenti davvero, il migliore che abbia visto!

    Rispondi

Rispondi a Ilaria Barretta Annulla risposta

Il tuo indirizzo email non sarà pubblicato.