Esame di maturità 2024 prova di matematica – Prova svolta

Indice

Problema 1
Problema 2
Quesito 1
Quesito 2
Quesito 3
Quesito 4
Quesito 5
Quesito 6
Quesito 7
Quesito 8

Problema 1

Punto a

Per prima cosa calcoliamo la derivata della funzione $f_{a,b}(x)$ che è

$f'_{a,b}(x)={3ax^2\cdot x^2-(ax^3+b)\cdot 2x\over x^4}={ax^4-2bx\over x^4}$

a questo punto se vogliamo che la curva sia tangente alla retta $t$ nel punto di ascissa $x=1$ sicuramente dobbiamo avere che la curva e la retta passino dallo stesso punto per $x=1$ , ossia $P(1\:;\:5)$ e che la derivata in quel punto sia $f'_{a,b}(1)=-7$ . Pertanto

$f_{a,b}(1)=5\Rightarrow a+b=5$

$f'_{a,b}(1)=-7\Rightarrow a-2b=-7$

da cui $b=4$ e $a=1$ .

Ritorna all’indice

Punto b

Studiamo ora la funzione $f(x)={x^3+4\over x^2}$ . Sappiamo che il suo dominio è tutto l’insieme dei numeri reali meno lo $0$ . Vediamo ora i limiti nei punti estremi del dominio

$\lim_{x\to -\infty}{x^3+4\over x^2}=-\infty$

$\lim_{x\to +\infty}{x^3+4\over x^2}=+\infty$

Cerchiamo un possibile asintoto obliquo

$m=lim_{x\to \infty}{f(x)\over x}=lim_{x\to \infty}{x^3+4\over x^3}=1$

$q=lim_{x\to \infty}f(x)-mx=lim_{x\to \infty}{x^3+4\over x^2}-x=0$

per cui abbiamo un’asintoto obliquo di equazione $y=x$ . Cerchiamo ora un possibile asintoto verticale facendo i limiti per $x$ che tende a $0$

$\lim_{x\to 0^-}{x^3+4\over x^2}=+\infty$

$\lim_{x\to 0^+}{x^3+4\over x^2}=+\infty$

Cerchiamo infine i punti di massimo e minimo

$f'(x)=0\Rightarrow x=2$

da cui possiamo disegnare la funzione

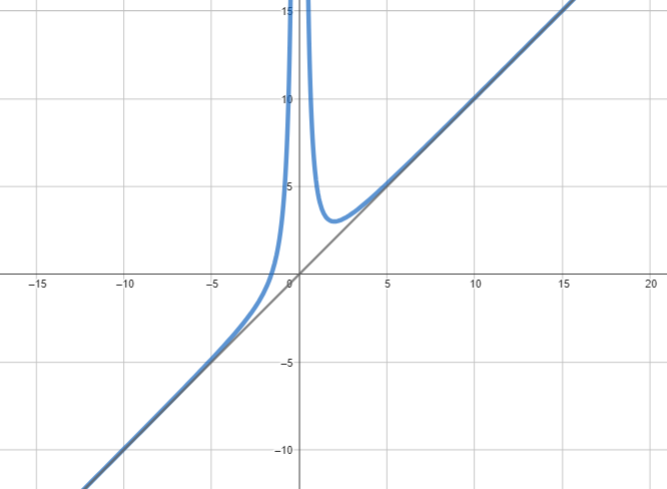
Completiamo ora il punto b) scrivendo l’equazione dell’ulteriore retta tangente alla curva e passante per $P$ , osserviamo anche che tale retta non sarà tangente nel punto $P$ , ma semplicemente passerà per tale punto. La retta tangente in un generico punto $A=(a\:;\:{a^3+4\over a^2})$ con $a\neq 0$ ha equazione

$y-{a^3+4\over a^2}=(1-{8\over a^2})(x-a)$

pertanto, imponendo il passaggio per il punto $P$ otteniamo

$5-{a^3+4\over a^2}=(1-{8\over a^2})(1-a)$

da cui si ottiene

$a^3-3a+2=0\Rightarrow (a-1)^2(a+2)=0\Rightarrow a=-2\:e\:a=1$

pertanto la seconda retta tangente passa, ed è tangente, al punto $Q(-2\:;\:-1)$ ed ha equazione

$y+1=2(x+2)\Rightarrow y=2x+3$

Ritorna all’indice

Punto c

Per risolvere questo punto mettiamo a sistema l’equazione del fascio $y-5=m(x-1)$ e l’equazione della curva. Risolviamo per sostituzione sostituendo $y=5+m(x-1)$ e otteniamo

$5+m(x-1)={x^3+4\over x^2}$

$5x^2+mx^3-mx^2=x^3+4$

$(m-1)x^3+(5-m)x^2-4=0$

Ragioniamo ora sulle soluzioni di quell’equazione di terzo grado. Vediamo subito che per $m=1$ l’equazione diventa l’equazione di secondo grado $x^2-1=0$ , pertanto abbiamo due soluzioni. Per $m<1$ il coefficiente direttore $m-1$ è negativo e siccome tale polinomio passa dal punto $(0\:;\:-4)$ ne consegue che deve necessariamente avere tre soluzioni, pertanto per $m<1$ le soluzioni sono tre. Con $1<m<2$ si hanno tre soluzioni distinte. Mentre quando $m=2$ l’equazione di terzo grado $x^3+3x^2-4=0$ ha due soluzioni coincidenti e quando $m$ diventa maggiore di $2$ si ha un’unica soluzione reale.

Ritorna all’indice

Punto d

Quello che ci viene chiesto di calcolare è l’area della regione arancione presente in questo grafico man mano che la retta di equazione $x=k$ si sposta sempre più a destra

geometricamente possiamo subito osservare che tale limite dovrà tendere a un numero proprio per definizione di asintoto obliquo. Vediamo questo dal punto di vista analitico. L’area della figura arancione la possiamo calcolare facendo

$\lim_{k\to +\infty}(\int_1^{3\over 2}{x^3+4\over x^2}-(-7x+12)dx+\int_{3\over 2}^k {x^3+4\over x^2}-xdx)$

$\lim_{k\to +\infty}(\int_1^{3\over 2}8x+{4\over x^2}-12dx+\int_{3\over 2}^k {4\over x^2}dx)$

$\lim_{k\to +\infty}(4\cdot \Big[x^2-{1\over x}-3x\Big]_1^{3\over 2}+{8\over 3}-{4\over k})$

$\lim_{k\to +\infty}({1\over 3}+{8\over 3}-{4\over k})=3$

Ritorna all’indice

Problema 2

Punto a

Per verificare che la famiglia di funzioni $f_n(x)$ non è derivabile nel punto di ascissa $x=0$ calcoliamo il limite del rapporto incrementale da destra e da sinistra e verifichiamo come si comporta. Innanzitutto abbiamo che

$f_n(x)=\sqrt[n]{x^2}-\sqrt{ax^2+bx+1}=x^{2\over n}-(ax^2+bx+1)^{1\over 2}$

pertanto in un intorno di $x=0$ la funzione è perfettamente definita e quindi possiamo dire che

$f'_n(x)={2\over n}\cdot x^{{2\over n}-1}-{1\over 2}\cdot (ax^2+bx+1)^{{1\over 2}-1}\cdot (2ax+b)$

A questo punto separiamo i due casi $n=2$ e $n>2$ . Nel primo caso, con $n=2$ , la funzione diventa

$f_2(x)=\left | x \right |-\sqrt{ax^2+bx+1}$

che quindi derivata diventa per $x<0$

$f'_2(x)=-1-{1\over 2}\cdot (ax^2+bx+1)^{-{1\over 2}}\cdot (2ax+b)$

e per $x>0$

$f'_2(x)=1-{1\over 2}\cdot (ax^2+bx+1)^{-{1\over 2}}\cdot (2ax+b)$

quindi il limite destro e il limite sinistro sono diversi, infatti

$\lim_{x\to 0^-}f_2(x)=\lim_{x\to 0^-}-1-{1\over 2}\cdot (ax^2+bx+1)^{-{1\over 2}}\cdot (2ax+b)=-1-{b\over 2}$

$\lim_{x\to 0^+}f_2(x)=\lim_{x\to 0^+}1-{1\over 2}\cdot (ax^2+bx+1)^{-{1\over 2}}\cdot (2ax+b)=1-{b\over 2}$

Analizziamo ora il secondo caso, cioè $n>2$ , in questa situazione il primo termine della derivata diventa

${2\over n}\cdot x^{{2\over n}-1}={2\over nx^{n-2\over n}}$

pertanto il limite sinistro viene

$\lim_{x\to 0^-}f_n(x)=\lim_{x\to 0^-}{2\over nx^{n-2\over n}}-{1\over 2}\cdot (ax^2+bx+1)^{-{1\over 2}}\cdot (2ax+b)=\pm\infty$

dove il più lo abbiamo nel caso in cui $n$ sia pari, mentre il segno meno nel caso in cui $n$ sia dispari. Per il limite destro invece abbiamo il risultato sempre positivo, ossia

$\lim_{x\to 0^+}f_n(x)=\lim_{x\to 0^+}{2\over nx^{n-2\over n}}-{1\over 2}\cdot (ax^2+bx+1)^{-{1\over 2}}\cdot (2ax+b)=+\infty$

Questo ragionamento ci fornisce anche la risposta ai punti angolosi, infatti tali punti li abbiamo quando i limiti sono diversi, pertanto quando $n$ è un numero dispari oppure quando $n=2$ .
Determiniamo ora i parametri $a, b$ in maniera tale che il grafico sia quello in figura

Siccome deve essere simmetrico rispetto all’asse $y$ abbiamo che

$f_2(x)=f_2(-x)$

pertanto

$\left | x \right |-\sqrt{ax^2+bx+1}=\left | -x \right |-\sqrt{a(-x)^2-bx+1}$

$\sqrt{ax^2+bx+1}=\sqrt{ax^2-bx+1}$

per cui necessariamente $b=0$ , per determinare il valore di $a$ imponiamo che il dominio sia $[-1\:;\:1]$ , quindi risolviamo la disequazione

$ax^2+1\geq 0\Rightarrow x\in[-{1\over \sqrt{a}}\:;\:+{1\over \sqrt{a}}]$

pertanto se vogliamo che quell’intervallo sia $[-1\:;\:1]$ dobbiamo avere $a=-1$ .

Ritorna all’indice

Punto b

Studiamo ora la funzione

$g(x)=\left | x \right |+\sqrt{1-x^2}$

ancora una volta il suo dominio è la soluzione della disequazione $1-x^2\geq 0$ pertanto è l’intervallo $[-1\:;\:1]$ . Inoltre la sua derivata è

$g'(x)=\mp 1-{2x\over 2\sqrt{1-x^2}}$

dove il segno meno lo abbiamo quando $x<0$ mentre il segno più quando $x>0$ . Pertanto

$lim_{x\to -1^+}g'(x)=lim_{x\to -1^+} -1-{2x\over 2\sqrt{1-x^2}}=+\infty$

$lim_{x\to +1^-}g'(x)=lim_{x\to +1^-} 1-{2x\over 2\sqrt{1-x^2}}=-\infty$

quindi negli estremi del dominio la funzione non è derivabile, vediamo ora come si comporta per $x=0$ .

$lim_{x\to 0^-}g'(x)=lim_{x\to 0^-} -1-{2x\over 2\sqrt{1-x^2}}=-1$

$lim_{x\to 0^+}g'(x)=lim_{x\to 0^-} 1-{2x\over 2\sqrt{1-x^2}}=+1$

pertanto neanche nel punto $x=0$ la funzione non è derivabile. Una volta verificato questo procediamo con lo studio di funzione, l’unica cosa che ci manca per poter disegnare la funzione $g(x)$ è lo studio della derivata prima per poter determinare le concavità e i massimi e minimi, quindi studiamo $g(x)>0$ . Per $x<0$ abbiamo

$-1-{2x\over 2\sqrt{1-x^2}}>0\Rightarrow x<-{1\over \sqrt 2}$

quindi nel punto $x=-{1\over \sqrt 2}$ abbiamo un massimo relativo. Per completare osserviamo che $g(x)$ è una funzione pari, pertanto il suo grafico è simmetrico rispetto all’asse $y$ . Una volta fatto questo disegniamo i due grafici uniti

Ritorna all’indice

Punto c

I punti di intersezione tra la retta $x=k$ e la nostra curva a cuore sono le intersezioni tra le due curve con la retta (infatti nella parte bassa del cuore la curva blu è rappresentata dalla curva $f(x)$ mentre nella parte alta del cuore la curva rossa è rappresentata dalla curva $g(x)$ ). Pertanto le coordinate $y$ dei due punti di intersezione sono $f(k)$ e $g(k)$ , osserviamo anche che siccome entrambe le funzioni sono pari a noi basta studiare la situazione per $k\in[0\:;\:1]$

$f(k)=k-\sqrt{1-k^2}$

$g(k)=k+\sqrt{1-k^2}$

quindi la formula che esprime la distanza tra questi due punti sarà

$g(k)-f(k)=k+\sqrt{1-k^2}-(k-\sqrt{1-k^2})=2\sqrt{1-k^2}$

che è una funzione strettamente decrescente e quindi ha il massimo per $k=0$ .

Ritorna all’indice

Punto d

Per verificare che $H(x)$ è una primitiva di $h(x)$ ci basta derivare $H(x)$ e vedere che, a meno di una costante, viene $h(x)$ . Quindi

$H'(x)={1\over 2}({1\over \sqrt{1-x^2}}+1\cdot \sqrt{1-x^2}-x\cdot {2x\over 2\sqrt{1-x^2}})={1\over 2}({1+1-x^2-x^2\over \sqrt{1-x^2}})={1\over 2}({2-2x^2\over \sqrt{1-x^2}})=h(x)$

Infine per calcolare l’area del cuore impostiamo i seguenti integrali

$A=2\cdot (\int_0^1(g(x)-f(x))dx)=2\int_0^12\sqrt{1-x^2}dx=4\cdot \Big[H(x)\Big]_0^1$

$A=\Big [\arcsin x+x\sqrt{1-x^2}\Big]_0^1=2(\arcsin 1-\arcsin0)=\pi$

Ritorna all’indice

Quesito 1

Partiamo con la prima parte della dimostrazione. Sia quindi $ABC$ un triangolo rettangolo isoscele e vediamo che la sua altezza relativa all’ipotenusa deve essere la metà dell’ipotenusa.

Sicuramente l’angolo in $C$ è un angolo di $45^\circ$ , siccome il triangolo grande è un triangolo isoscele e rettangolo, e sicuramente l’angolo $BHC$ è un angolo retto siccome $BH$ è altezza, ne segue che anche l’angolo $HBC$ è di $45^\circ$ e pertanto il triangolo $BCH$ è isoscele. Quindi possiamo concludere che la lunghezza di $BH$ e la lunghezza di $HC$ coincidono, ma sappiamo già che $HC$ è la metà di $AC$ in quanto nei triangoli isosceli l’altezza relativa alla base è anche mediana.
Proviamo ora l’implicazione opposta, ossia $ABC$ è un triangolo rettangolo tale che l’altezza relativa all’ipotenusa sia esattamente la metà dell’ipotenusa allora $ABC$ è anche isoscele. Se ci rifacciamo sempre all’immagine di prima abbiamo come ipotesi che $\bar{BH}=\bar{HC}=\bar{HA}$ inoltre anche gli angoli $BHC$ e $BHA$ sono congruenti perchè $BH$ è altezza, ne segue che i due triangoli $BCH$ e $BHA$ sono congruenti e pertanto i due angoli adiacenti all’ipotenusa di $ABC$ sono congruenti da cui segue che $ABC$ è isoscele.

Ritorna all’indice

Quesito 2

I modi di ottenere esattamente due testa in cinque lanci sono $10$ (ad esempio $TTCCC$ , $TCTCC$ , $TCCTC$ e così via), pertanto la probabilità di ottenere esattamente due teste è

$10\cdot p^2\cdot (1-p)^3$

Per rispondere alla seconda domanda, siccome ci chiede un massimo, basta cercare i massimi della funzione probabilità, quindi come prima cosa la deriviamo in $p$ e otteniamo

$10\cdot (2p(1-p)^3-3p^2(1-p)^2)=10p(1-p)^2(2-5p)$

per cui la derivata ha tre zeri che sono $p=0$ , $p=1$ e $p=2/5$ . Le prime due soluzioni sono quelle che rendono nulla la probabilità che escano esattamente due teste, mentre la terza soluzione $p=2/5$ è quella che rende massima la probabilità che escano esattamente due teste.

Ritorna all’indice

Brevi lezioni

Esame di maturità 2024 prova di matematica – Prova svolta

Indice

Problema 1

Problema 2

Quesito 1

Quesito 2

Quesito 3

Quesito 4

Quesito 5

Quesito 6

Quesito 7

Quesito 8

Lascia un commento Annulla risposta