Archivi categoria: Vettori e forze

Esercizio 14 sui vettori e le forze – Esercizi svolti – FISICA

La forza orizzontale necessaria per mettere in movimento un tavolo di massa $m=15\: kg$ è $F=45\:N$ . La forza necessaria per mantenerlo in movimento è inferiore del $15\: \%$ . Trascurando la presenza dell’aria determina il valore del coefficiente di attrito dinamico.

SVOLGIMENTO

Il coefficiente di attrito dinamico è un numero adimensionale che verifica sperimentalmente la seguente relazione:

$\mu_d={F_a \over F_\bot}$

da cui possiamo facilmente calcolare

$\mu_d={F\cdot 0,85 \over m\cdot g}={45\:N\cdot 0,85 \over 15\: kg\cdot 9,81\: N/kg}\approx 0,26$

Visualizza la soluzione

Esercizi di fisica, Vettori e forze

Esercizio 13 sui vettori e le forze – Esercizi svolti – FISICA

Lascia un commento

Un lampadario di massa $3,0\: kg$ è appeso a un’asta orizzontale collegata al soffitto da due molle identiche agganciate alle sue estremità. Ciascuna delle molle si allunga di $5,0\: cm$ rispetto alla condizione di equilibrio. Quale è la costante elastica delle molle se la massa dell’asta è trascurabile?

SVOLGIMENTO

La forza peso del lampadario è assorbita dalle due molle che quindi si divideranno l’onere in parti uguali, quindi l’allungamento di $5,0\: cm$ è causato da metà della forza peso del lampadario, da cui:

$F_{elastica}=\Delta x \cdot k \Rightarrow k={F_{elastica}\over \Delta x}={m\cdot g\cdot{1\over 2} \over \Delta x}$

$k=={3,0\: kg\cdot 9,81\:N/kg\cdot{1\over 2}\over 0,05\: m}\approx 294\:N/m$

Visualizza la soluzione

Esercizi di fisica, Vettori e forze

Esercizio 12 sui vettori e le forze – Esercizi svolti – FISICA

Lascia un commento

Un libro viene premuto al muro con una forza perpendicolare. La massa del libro è $420\: g$ e il coefficiente di attrito statico con il muro vale $\mu_s =0,30$ . Calcola il valore minimo della forza che impedisce al libro di scivolare.

SVOLGIMENTO

Sul libro agisce la sua forza peso, che è quella che tende a far cadere il libro, mentre la forza di attrito è la forza che tiene il libro contro al muro sollevato da terra, la forza peso ha modulo:

$F_p=m\cdot g= 0,420\: kg\cdot 9,81\: N/kg\approx 4,1\: N$

mentre la forza perpendicolare per generare una forza di attrito di tale intensità si calcola con la formula

$\mu_s={F_a\over F_\bot}\Rightarrow F_\bot={F_a\over \mu_s}={4,1\:N \over 0,30 }\approx 13,7\: N$

Visualizza la soluzione

Esercizi di fisica, Vettori e forze

Esercizio 11 sui vettori e le forze – Esercizi svolti – FISICA

Lascia un commento

Anna sta stirando una maglia di lana. Tiene il ferro da stiro con il braccio inclinato a un angolo di $30^\circ$ rispetto al piano orizzontale esercitando una forza di $30\: N$ . Il coefficiente di attrito statico in questo caso vale $0,78$ e il ferro da stiro ha una massa di $1,2\: kg$ . Calcola il modulo della forza premente $F_\bot$ , Anna riuscirà a mettere il ferro da stiro in movimento?

SVOLGIMENTO

Vediamo immediatamente che la forza che Anna esercita sul ferro da stiro viene una parte contrastata dalla reazione vincolare del piano d’appoggio e una parte contrastata dalla forza di attrito. In particolare abbiamo che

$F_\bot=F_p+F_{anna}\cdot \sin(30^\circ)=1,2\: kg\cdot 9,81\: N/kg+30\:N\cdot \sin(30^\circ)\approx 26,8\: N$

Quindi la forza di attrito tra ferro e maglia sarà

$F_{attrito}=F_\bot\cdot \mu=26,8\: N\cdot 0,78=20,9\: N$

mentre la forza con cui Anna spinge il ferro da stiro lungo la direzione parallela è

$F_\parallel=F_{anna}\cdot \cos(30^\circ)\approx 26,0\: N$

per cui Anna riesce a muovere il ferro da stiro.

Visualizza la soluzione

Esercizi di fisica, Vettori e forze

Esercizio 10 sui vettori e le forze – Esercizi svolti – FISICA

6 commenti

Agnese lancia dalla finestra un mazzo di chiavi, di massa $153\: g$ , a Michele. Nel lancio applica una forza di modulo $2,4\: N$ che forma un angolo di $45^\circ$ con direzione orizzontale ed è diretta verso il basso. Calcola il modulo della forza totale applicata al mazzo di chiavi.

SVOLGIMENTO

Le forze che agiscono sulle chiavi sono due: la forza peso e la forza impressa da Agnese alle chiavi, inoltre di queste due forze conosciamo tutto. Fissiamo pertanto un sistema cartesiano sulle chiavi e osserviamo che le due forze in questo sistema hanno coordinate:

$\vec{F_p}=(0\: ; \: -m\cdot g)$

$\vec{F_a}=2,4\: N\cdot(\cos(315^\circ)\: ; \:\sin(315^\circ))$

da cui

$\vec{F_p}+\vec{F_a}=(2,4\: N\cdot\cos(315^\circ)\: ; \: 2,4\: N\cdot\sin(315^\circ)-m\cdot g)$

per cui

$F_p+F_a=\sqrt{(2,4\: N\cdot\cos(315^\circ))^2+(2,4\: N\cdot\sin(315^\circ)-m\cdot g)^2}$

$=\sqrt{(2,4\: N\cdot\cos(315^\circ))^2+(2,4\: N\cdot\sin(315^\circ)-0,153\: kg\cdot 9,81\:N/kg)^2}\approx 3,6\: N$

Visualizza la soluzione

Esercizi di fisica, Vettori e forze

Esercizio 9 sui vettori e le forze – Esercizi svolti – FISICA

Lascia un commento

Il coefficiente di attrito radente tra una cassapanca di legno di massa $56\: kg$ e il pavimento è di $0,27$ . Quanto vale l’intensità della forza minima necessaria per mettere in movimento la cassapanca?

SVOLGIMENTO

Sappiamo che esiste una relazione tra forza d’attrito, forza perpendicolare e coefficiente di attrito e che questa relazione è

$\mu ={F_a \over F_\bot}$

da cui

$F_a=\mu\cdot F_\bot=\mu\cdot m \cdot g\approx 148\: N$

Visualizza la soluzione

Esercizi di fisica, Vettori e forze

Esercizio 8 sui vettori e le forze – Esercizi svolti – FISICA

1 commento

Un giocatore di baseball colpisce una palla di massa $145\: g$ . La forza che la mazza applica alla palla forma un angolo di $30^\circ$ con la direzione orizzontale ed è diretta verso l’alto. Il modulo della forza è $3,2\: N$ . Calcola il modulo della forza totale applicata alla palla.

SVOLGIMENTO

Per risolvere questa tipologia di esercizio bisogna ragionare sulle forze che sono applicate all’oggetto e cercare di capire le loro caratteristiche vettoriali, cioè modulo, direzione e verso, una volta fatto questo rimane solo da sommare le forze. Risulta quindi evidente che nella risoluzione di esercizi di questo tipo i disegni geometrici sono molto importanti per capire le caratteristiche dei vettori in gioco.
Le forze che agiscono sulla pallina da baseball sono due: forza peso e forza con cui è stata colpita. La forza peso è un vettore diretto verso il basso di modulo $F_p=m\cdot g$ , mentre le caratteristiche dell’altra forza ci sono state date nel testo dell’esercizio. Quindi se voglio scrivere le componenti delle due forze in un sistema cartesiano centrato sulla pallina avrò:

$\vec{F_p}=(0\: ; \: -m\cdot g)$

$\vec{F_c}=3,2\:N\cdot(\cos(30^\circ)\: ; \: \sin(30^\circ))$

da cui

$\vec{F_p}+\vec{F_c}=(3,2\:N\cdot\cos(30^\circ)\: ; \: 3,2\:N\cdot\sin(30^\circ) -m\cdot g)$

Quindi il modulo di tale vettore sarà

$F_p+F_c=\sqrt{(3,2\:N\cdot\cos(30^\circ))^2+(3,2\:N\cdot\sin(30^\circ) -m\cdot g)^2}=$

$=\sqrt{(3,2\:N\cdot\cos(30^\circ))^2+(3,2\:N\cdot\sin(30^\circ) -0,145\: kg \cdot 9,81\: N/kg)^2}\approx 2,78\: N$

Visualizza la soluzione

Esercizi di fisica, Vettori e forze

Esercizio 7 sui vettori e le forze – Esercizi svolti – FISICA

2 commenti

Tre fratelli si contendono un joystick per giocare con una console, tirando con forze di intensità $50\: N$ , $30\: N$ , $30\: N$ , come illustrato in figura.

Calcola la forza risultante e chi si guadagna il turno per giocare.

SVOLGIMENTO

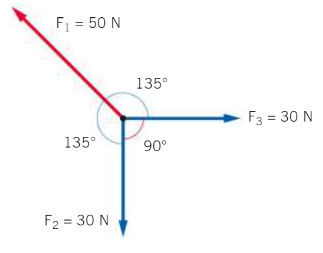
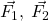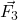Per calcolare la forza risultante bisogna sommare i tre vettori $\vec{F_1},\: \vec{F_2}$ e $\vec{F_3}$ . Per la particolarità della figura conviene utilizzare la proprietà associativa della somma di vettori e calcolare la risultante nel seguente modo:

$\vec{F_1}+\vec{F_2}+\vec{F_3}=\vec{F_1}+(\vec{F_2}+\vec{F_3})$

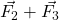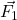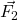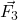questo perchè il vettore risultante $\vec{F_2}+\vec{F_3}$ sarà un vettore di direzione uguale a $\vec{F_1}$ e di verso opposto siccome $\vec{F_2}$ e $\vec{F_3}$ formano un quadrato e la diagonale del quadrato è anche bisettrice dell’angolo. Per cui

$F_2+F_3=\sqrt{F_2^2+F_3^2}\approx 42,43\: N$

$F_1+(F_2+F_3)=50\: N-42,43\: N=7,57\: N$

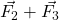Inoltre siccome abbiamo messo con il segno positivo il vettore $\vec{F_1}$ e con il segno negativo il vettore $\vec{F_2}+\vec{F_3}$ dal segno del risultato capiamo che la risultante sarà diretta nello stesso verso di $\vec{F_1}$ .
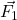Immaginiamo ora di non essere riusciti a notare il ragionamento appena fatto e ragioniamo sulle coordinate cartesiane dei tre vettori. Fissiamo quindi un piano cartesiano con i due assi nella stessa direzione di 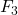$F_3$ e $F_2$ , allora in questo sistema le coordinate dei tre vettori saranno

$\vec{F}_1=50\: N\cdot (\cos{135^\circ}\:;\: \sin{135^\circ})$

$\vec{F}_2=(0\: ; \: -30\: N)$

$\vec{F}_3=(30\: N\: ; \: 0)$

Per cui

$\vec{F}_1+\vec{F}_2+\vec{F}_3=(50\: N\cdot\cos{135^\circ}+30\: N\: ;\: 50\: N\cdot\sin{135^\circ}-30\: N)\approx (-5,36\: N\: ;\: 5,36\: N )$

Quindi chiaramente un vettore di direzione e verso uguale a 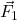$\vec{F}_1$ , e di modulo

$F_1+F_2+F_3=\sqrt{(-5,36\: N)^2+(5,36\: N)^2}\approx 7,57\: N$

esattamente gli stessi risultati ottenuti prima.

Visualizza la soluzione

Esercizi di fisica, Vettori e forze

Esercizio 6 sui vettori e le forze – Esercizi svolti – FISICA

3 commenti

Un astronauta utilizza una comune bilancia per pesarsi sulla Terra e sulla Luna. Sulla Terra la bilancia indica il valore $80\: kg$ ; la costante di gravità sulla Luna è $g_L=1,62\:N/kg$ . Quale valore indica la bilancia sulla Luna?

SVOLGIMENTO

Sappiamo che la bilancia è uno strumento di misura che misura la forza peso di un determinato oggetto, cioè la forza con cui un corpo celeste attrae un oggetto per gravità, e attraverso la relazione

$F_P=m\cdot g_T \Rightarrow m={F_P\over g_T}$

ricava la massa di un determinato oggetto (noto esplicitamente che le bilance utilizzano come dato $g_T$ perchè sono progettate per funzionare sulla Terra e non altrove). Ovviamente sulla Luna, di massa inferiore alla Terra, la forza gravitazionale è inferiore a quella sulla Terra, però concettualmente il calcolo della forza peso sarà sempre:

$F_{PL}=m\cdot g_L$

Per cui la bilancia segnerà come peso

$m={F_{PL}\over g_T}={m\cdot g_L \over g_T}\approx 13\: kg$

Visualizza la soluzione

Esercizi di fisica, Vettori e forze

Esercizio 5 sui vettori e le forze – Esercizi svolti – FISICA

Lascia un commento

In una gara di tiro della fune, Paolo, Carlo e Marco esercitano le forze rispettivamente di $560\: N$ , $480\: N$ e $600\: N$ verso sinistra, mentre Franco, Alessandro e Matteo le forze di $550\: N$ , $430\: N$ e $580\: N$ in verso opposto. Quale è la forza risultante?

SVOLGIMENTO

Dobbiamo fare una semplice somma di vettori e dobbiamo considerare che i vettori forza che stiamo sommando sono tutti sulla stessa direzione. Per prima cosa quindi determiniamo il verso positivo dei vettori e per convenzione (totalmente arbitraria) decidiamo che le forze applicate verso destra siano positive e le forze applicate verso sinistra siano negative, a questo punto risulta evidente che

$F_{risultante}=F_{Paolo}+F_{Carlo}+F_{Marco}+F_{Franco}+F_{Alessandro}+F_{Matteo}$

$F_{risultante}=-560\: N-480\: N-600\: N+550\: N+430\: N+580\: N=-80\: N$

Notiamo esplicitamente che il segno meno presente nel risultato indica esclusivamente il verso del vettore risultante che quindi sarà diretto verso sinistra.

Visualizza la soluzione