Un aliscafo percorre 
in 
e in seguito altri 
nelle 
seguenti. Quanto vale la sua velocità media sull’intero percorso?
Sappiamo che la velocità media è definita come
![\[v_m={\Delta x\over \Delta t}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-b576e66917ade2c452156ad9f90bde3e_l3.png "Rendered by QuickLaTeX.com")
ossia il tempo percorso fratto il tempo necessario per percorrerlo. A questo punto risulta facile capire che sia lo spazio che il tempo lo dobbiamo spezzare nei due tragitti, da cui otteniamo
![\[v_m={\Delta x_1+\Delta x_2\over \Delta t_1+\Delta t_2}={100\: km+100\: km\over 2,0\: h+3,0\: h}=40\: km/h\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9fe68df9ea6cd1962101764d74763a5a_l3.png "Rendered by QuickLaTeX.com")
 | TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME |  |
Una nave si dirige alla velocità di 
verso un’altra nave attraccata al largo. Quando la distanza fra loro è di 
, la prima nave segnala la sua presenza con un fischio della sirena (la velocità del suono in aria è 
). La seconda nave risponde a sua volta con un altro fischio di sirena appena sente il fischio della prima nave.
– Di quanto si è avvicinata la prima nave tra l’emissione del primo fischio e la sua ricezione?
– Quanto tempo è trascorso fra l’emissione del primo fischio e la ricezione del secondo?
L’esercizio si basa tutto sul fatto che il suono non si propaga in maniera istantanea, anzi ha una velocità nell’aria di 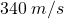. Vediamo pertanto come impostare la risoluzione del problema tenendo conto di questo dettaglio.
Per impostare la risoluzione cerchiamo di formalizzare quello che sappiamo:
1) sicuramente durante il tempo in cui il primo fischio si muove la nave 1 si avvicina alla nave 2, in particolare
![\[\Delta x_{nave\:1}+\Delta x_{fischio}=2\: km\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-ef0a9442201d6a8e4edad899a7b0f4c5_l3.png "Rendered by QuickLaTeX.com")
ossia lo spazio che separava le due navi al momento del fischio era di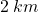 
.
2) La nave 1 si avvicina con una velocità di
![\[v=36\: km/h\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-5ed038b1cc4c846346571c4a9b7a7197_l3.png "Rendered by QuickLaTeX.com")
3) I due spazi descritti nel punto 1), ossia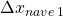 
e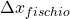 
, sono stati percorsi nello stesso tempo che chiameremo 
.
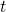4) La velocità del suono è
![\[340\: m/s=1224\: km/h\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-1ceb342147f19e5ba3f1b9b0440fcf9d_l3.png "Rendered by QuickLaTeX.com")
A questo punto, utilizzando l’osservazione 3) e la definizione di velocità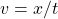 
, risulta che
![\[t_{nave}=t_{fischio}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-7d3620662d60e024df6f51e41b6a77f1_l3.png "Rendered by QuickLaTeX.com")
![\[{\Delta x_{nave\:1}\over v}={2\: km-\Delta x_{nave\:1}\over v_s}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-a4d705f77e9496e6a7c049d48e200def_l3.png "Rendered by QuickLaTeX.com")
![\[{\Delta x_{nave\:1}\over v}={2\: km\over v_s}-{\Delta x_{nave\:1}\over v_s}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-335021f33f483e68ff17ec15d70a7696_l3.png "Rendered by QuickLaTeX.com")
![\[{\Delta x_{nave\:1}\over v}+{\Delta x_{nave\:1}\over v_s}={2\: km\over v_s}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8194549ff44a247100f7d437aef70a43_l3.png "Rendered by QuickLaTeX.com")
![\[\Delta x_{nave\:1}\cdot ({1\over v}+{1\over v_s})={2\: km\over v_s}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-4dc710f57642b11c077e0f2fa95651a6_l3.png "Rendered by QuickLaTeX.com")
![\[\Delta x_{nave\:1}={2\: km\over v_s\cdot ({1\over v}+{1\over v_s}) }\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-07def369811159255770fa5464b12f55_l3.png "Rendered by QuickLaTeX.com")
![\[\Delta x_{nave\:1}={2\: km\over 1224\: km/h\cdot ({1\over 36\:km/h}+{1\over 1224 \: km/h}) }\approx 0,057\: km\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-46d45f9b582545694398b681f12efe35_l3.png "Rendered by QuickLaTeX.com")
Per rispondere alla seconda domanda utilizziamo il calcolo fatto nel punto 1, infatti sapendo la distanza percorsa dalla nave e la sua velocità possiamo facilmente calcolare il tempo che impiega il primo fischio per raggiungere la nave (convertiamo opportunamente la velocità in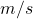 
e la distanza in 
):
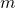![\[t_1={s_1\over v}={57\: m\over 10\: m/s}\approx 5,7\: s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-a54c237ea831006287b97c042c32c8bd_l3.png "Rendered by QuickLaTeX.com")
Per calcolare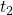 
utilizziamo la formula vista nel punto 1 che utilizzi al posto che 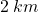il nuovo spazio 
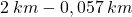per cui
![\[s_2={2\: km-0,057\: km \over 1224\: km/h\cdot ({1\over 36\:km/h}+{1\over 1224 \: km/h}) }\approx 0,056\: km\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-cd79756c1278743be986ec13df08de8b_l3.png "Rendered by QuickLaTeX.com")
![\[t_2={s_2\over v}={56\: m\over 10\: m/h}\approx 5,6\: s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-097569f37de2d778b197e279b742a78c_l3.png "Rendered by QuickLaTeX.com")
da cui
![\[t_{tot}=t_1+t_2=5,7\:s+5,6\:s=11,3\: s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-03d4d02e9eb404a3331735b95bc374b1_l3.png "Rendered by QuickLaTeX.com")
| TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME | |
Uno yo-yo impiega 
a scendere di 
e 
per risalire di 
. Considera positivo il verso in cui avviene la salita. Calcola la velocità media:
– nel tratto in discesa;
– nel tratto in salita;
– su tutto il percorso.
Sappiamo che la velocità media è definita come
ovvero spazio percorso fratto il tempo impiegato per percorrerlo. Pertanto
![\[v_m^{discesa}={-0,75\: m\over 1,5\:s}=-0,5\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-485697599e23c6681d93f6b99bec86db_l3.png "Rendered by QuickLaTeX.com")
![\[v_m^{salita}={0,60\: m\over 1,8\:s}\approx 0,3\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-26de10b47e5d48f84f636445a1b68b8f_l3.png "Rendered by QuickLaTeX.com")
![\[v_m^{totale}={(0,75-0,6)\: m\over (1,8+1,5)\:s}\approx 0,045\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-05a25f7f744814968cc998dfe7ed9c0a_l3.png "Rendered by QuickLaTeX.com")
Dove osserviamo esplicitamente che 
rappresenta un vettore, pertanto il segno di ci dice semplicemente se lo spostamento avviene lungo la direzione positiva oppure lungo la direzione negativa.
| TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME | |
La posizione di una particella in funzione del tempo è:
![\[x(t)=(3,1\: m/s)\cdot t-(4,2\: m/s^2)\cdot t^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-0d9b78eb37e18f693693573de80d6be8_l3.png "Rendered by QuickLaTeX.com")
e 
.
Nonostante questo non sia un moto a velocità costante per il calcolo della velocità media questo non ci interessa, infatti la velocità media, a prescindere dal tipo di moto che stiamo esaminando, si calcola facendo:
ossia spazio percorso fratto il tempo necessario a percorrerlo. In questo esercizio ci viene fornita quella che in termini fisici si chiama la legge orario del moto, ossia una formula che ci permette di terminare la posizione in funzione del tempo. In particolare possiamo calcolare
![\[\Delta x=x(2)-x(1)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-321e7b8d2c58ca3cefbe99482d948558_l3.png "Rendered by QuickLaTeX.com")
![\[=(3,1\: m/s)\cdot 2\:s-(4,2\: m/s^2)\cdot (2\:s)^2-(3,1\: m/s)\cdot 1\:s-(4,2\: m/s^2)\cdot (1\:s)^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-ac064c65f71a3e3119bc93fd84d74a8e_l3.png "Rendered by QuickLaTeX.com")
![\[=-10,6\: m-(-1,1\:m)=-9,5\: m\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-b4fbd1497ab80b4c238404696813a2fe_l3.png "Rendered by QuickLaTeX.com")
Non ci deve dare nessun problema il segno negativo del , infatti tale segno semplicemente sta a significare che il movimento del corpo è di verso contrario a quello che abbiamo considerato come verso positivo.
In definitiva quindi
![\[v_m={\Delta x\over \Delta t}={x(2)-x(1)\over t_f-t_i}={-9,5\: m\over 1\: s}=-9,5\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8b2a92079f9441aceb8c08e95a0566e9_l3.png "Rendered by QuickLaTeX.com")
| TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME | |
In una strada trafficata, durante l’ora di punta, guidi un’automobile in linea retta a 
per 
, poi rimani fermo per 
e infine procedi a 
per altri 
. Determina la velocità media fra 
e 
.
Ricordiamo la definizione di velocità media, ossia
ovvero lo spazio percorso fratto il tempo necessario a percorrerlo. Osserviamo che l’automobile percorre strada solamente nel primo e nel terzo periodo, ciò non toglie però che anche il secondo periodo vada considerato all’interno del tempo totale. Consideriamo pertanto il tempo diviso in tre parti e calcoliamo lo spazio percorso in ognuna di queste parti.
![\[\Delta x_1=v_1\cdot t_1=12\: m/s\cdot 90\:s=1080\: m\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-bdd0aea1c18c5e36d5e1f16b3c9a24ac_l3.png "Rendered by QuickLaTeX.com")
![\[\Delta x_2=v_2\cdot t_2=0\: m/s\cdot 210\: s=0\:m\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-bb6f05eea8285f16c123764112c5fee6_l3.png "Rendered by QuickLaTeX.com")
![\[\Delta x_3=v_3\cdot t_3=15\: m/s\cdot 150\: s=2250\: m\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-3ecc042d6373a35570fb5c8f2ecf3b71_l3.png "Rendered by QuickLaTeX.com")
Dove osserviamo che il tempo deve essere convertito in secondi per poter operare il calcolo. A questo punto otteniamo
![\[v_m={1080\: m+0\: m+2250\: m\over 450\: s}= 7,4\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-47ed1f2969fcfd29bbe203dd9451a1f4_l3.png "Rendered by QuickLaTeX.com")
| TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME | |
Nella fase finale di una maratona il telecronista informa che il gruppo dei primi sta correndo a 
(ovvero percorre 
in 
). Esprimi la loro velocità in e 
.
La velocità è definita come
![\[v={\Delta x\over \Delta t}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-1260d25153aff84e1f128c6d09529560_l3.png "Rendered by QuickLaTeX.com")
ossia lo spazio percorso fratto il tempo necessario a percorrerlo. In questo particolare esercizio il maratoneta percorre 
in 
, una volta fatte queste considerazioni e conversioni risulta evidente che
![\[v={1\: km\over 0,047\: h}\approx 21,3\: km/h\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-552dc6e4aa4c129415c93746d075291d_l3.png "Rendered by QuickLaTeX.com")
![\[v={1000\: m\over 170\:s}\approx 5,9\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-ac5f8e52d3485ecdb9bc041384277ece_l3.png "Rendered by QuickLaTeX.com")
Osserviamo esplicitamente che abbiamo deciso di utilizzare due volte la formula, prima con i chilometri e le ore, e poi con i metri e i secondi, ma avremmo potuto anche fare l’equivalenza tra e .
| TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME | |
A Firenze, un turista percorre la distanza tra la stazione di Santa Maria Novella e Pizza della Signoria in 
. Questa distanze è di circa . Qual è la velocità media in del turista sull’intero tragitto? A quanti equivale?
Sappiamo che la velocità media è definita come
ossia spazio percorso fratto il tempo necessario a percorrerlo, pertanto per poter calcolare la velocità media in questo esercizio facciamo
![\[v_m={1000\: m\over 900\: s}\approx 1,1\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-e2bf271152ba2ececbc2a743fbd846e9_l3.png "Rendered by QuickLaTeX.com")
Per rispondere alla seconda domanda non ci resta che convertire la velocità in , ossia
![\[1,1\: m/s=1,1\cdot 3,6\: km/h\approx 4\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-80bc7f88efda5ab9786640c91151bb10_l3.png "Rendered by QuickLaTeX.com")
Osserviamo esplicitamente che il conto 
da circa come risultato 
, però la velocità in di questo esercizio è esattamente 
, infatti se utilizzassimo la formula della velocità media con i chilometri e le ore verrebbe
![\[v_m={1\: km\over 0,25\; h}=4\: km/h\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-5dd17d01bfc36d8e8c150de9070c82da_l3.png "Rendered by QuickLaTeX.com")
| TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME | |
La finale dei 
piani in una gara internazionale viene corsa in circa 
. Qual è la velocità media dell’atleta in ?
Sappiamo che la velocità media si calcola facendo
pertanto
![\[v_m={100\: m\over 10\:s}=10\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-567db4c1074584cb24b06dc3c233cbc5_l3.png "Rendered by QuickLaTeX.com")
dove osserviamo esplicitamente che, siccome abbiamo messo dentro alla formula dei metri e dei secondi, l’unità di misura sarà . Una volta ottenuto questo risultato non ci resta che convertirlo in , ossia
![\[v_m=10\: m/s=10\cdot 3,6\: km/h=36\: km/h\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-1bc8c867c89f78f0ae6b11237e113975_l3.png "Rendered by QuickLaTeX.com")
| TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME | |
Il 14 aprile 2013 Fernando Alonso, nella scuderia Ferrari, ha vinto il Gran Premio di Cina a Shangai, percorrendo 
in 
. Ogni giro del circuito è lungo 
. Calcola la velocità media tenuta dal ferrarista, esprimendola in .
Sappiamo che la velocità media è definita come
ossia spazio percorso fratto il tempo necessario per percorrerlo, inoltre sappiamo che se vogliamo il risultato in dobbiamo inserire lo spazio in chilometri e il tempo in ore. Pertanto calcoliamo e 
![\[\Delta x=56\: giri\cdot 5,4\: {km\over giro}=302,4\: km\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-a4698672e581383ff96028723d15ef7e_l3.png "Rendered by QuickLaTeX.com")
![\[\Delta t=1\:h+36\: min+26,9\:s=1\:h+{36\over 60}\:h+{26,9\over 3600}\: h\approx 1,607\: h\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8e152b28e4059887db833d2b8422eacb_l3.png "Rendered by QuickLaTeX.com")
da cui
![\[v_m={302,4\: km\over 1,607\:h}\approx 188,18\: km/h\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-df6b603fb7038cba265c38664083b3f3_l3.png "Rendered by QuickLaTeX.com")
| TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME | |
Un fringuello si posa sulla schiena di una tartaruga delle Galapagos, che cammina al maestoso passo di 
. Dopo 
il fringuello, stanco del passo lento della tartaruga, prende il volo nella stessa direzione e nello stesso verso per altri , con una velocità di . Qual è la velocità media del fringuello in questo intervallo di tempo di 
?
Sappiamo che la velocità media si calcola con la formula
ossia lo spazio percorso fratto il tempo necessario a percorrerlo. Quindi per poter utilizzare questa formula ci basta calcolare , in quanto 
.
Allora
![\[\Delta x=\Delta x_1+\Delta x_2=v_1\cdot \Delta t_1+v_2\cdot \Delta t_2=0,060\: {m\over s}\cdot 72\:s+12\:{m\over s}\cdot 72\:s=868,32\: m\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-b95f770c2c35b479b0e6f9f8ee50906f_l3.png "Rendered by QuickLaTeX.com")
da cui
![\[v_m={868,32\: m\over 144\:s}=6,03\: m/s\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-f2224beca8395a85ebf133894796e685_l3.png "Rendered by QuickLaTeX.com")
Osserviamo che in questo particolare esercizio la velocità media coincide con la media delle velocità, questo è dovuto esclusivamente al fatto che i due sono uguali.
| TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUL MOTO RETTILINEO UNIFORME | |