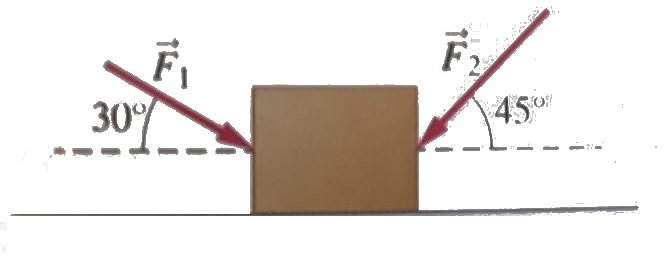
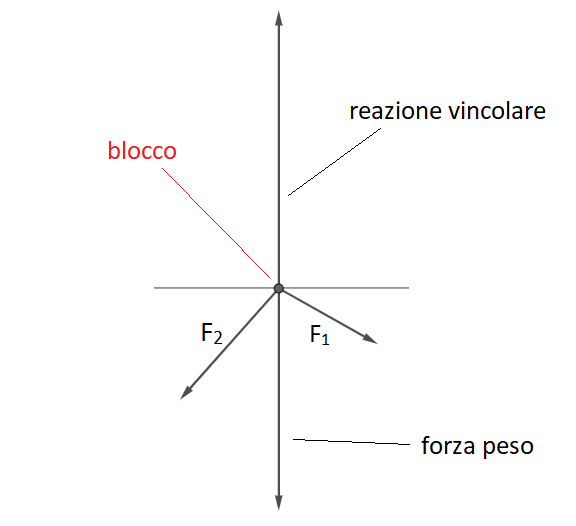
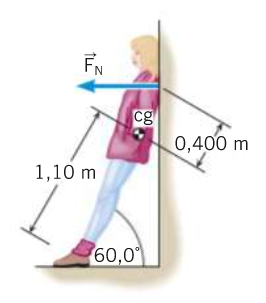
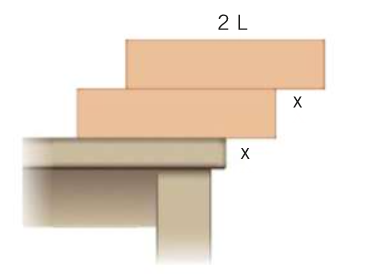
Se vogliamo far ruotare il blocco e non vogliamo che scorra sulla superficie orizzontale allora la forza applicata al blocco deve essere minore o uguale della forza di attrito, ossia
![Rendered by QuickLaTeX.com \[F\leq F_a\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-c7cc5ddf60ed50dcd972164ea50617e6_l3.png)
![Rendered by QuickLaTeX.com \[F\leq m\cdot g\cdot \mu\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-205051a235fcfb55bb14837e4b4cfc9a_l3.png)
Una forza di tale modulo mi permette sicuramente di non avere uno scorrimento del blocco di legno sulla superficie orizzontale, mentre per avere una rotazione deve risultare che tale forza generi un momento di modulo superiore al momento della forza peso del blocco, ossia
![Rendered by QuickLaTeX.com \[M_p\leq M_F\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-12aac8cce56d32d2b7b481f846e2e4c1_l3.png)
dove, supponendo il blocco omogeneo e quindi tale che il suo baricentro sia posizionato nell’incrocio delle diagonali del parallelepipedo, risulterà
![Rendered by QuickLaTeX.com \[{l\over 2}\cdot m\cdot g\leq b_F\cdot F\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-f820ffdebeec266b648ce7ecfceb582c_l3.png)
Queste sono le condizioni teoriche che devono essere rispettate dalla forza 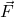 e dal braccio della forza
e dal braccio della forza 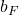 per risolvere il problema; le soluzioni a questo problema sono molteplici, numericamente calcoliamo solo la soluzione dove il modulo della forza
per risolvere il problema; le soluzioni a questo problema sono molteplici, numericamente calcoliamo solo la soluzione dove il modulo della forza 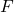 è il più grande possibile ed è pertanto applicato nel punto più basso possibile. Quindi
è il più grande possibile ed è pertanto applicato nel punto più basso possibile. Quindi
![Rendered by QuickLaTeX.com \[F= m\cdot g\cdot \mu=0,350\: kg\cdot 9,81\: N/kg\cdot 0,32\approx 1,1\: N\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-70f97d8c9c9232ad2e424542d8079aa9_l3.png)
da cui
![Rendered by QuickLaTeX.com \[b_F\geq {{l\over 2}\cdot m\cdot g\over F}={{l\over 2}\cdot m\cdot g\over m\cdot g\cdot \mu}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-32d24cac6fb1572dac2bfd7297d19030_l3.png)
![Rendered by QuickLaTeX.com \[b_F\geq {l\over 2\cdot \mu}={0,042\: m\over 2\cdot 0,32}\approx 0,066\: m\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-930507f9980c1d421d0a2bb1caceb302_l3.png)
Pertanto il punto di applicazione deve essere più alto di 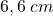 rispetto al punto di appoggio.
rispetto al punto di appoggio.
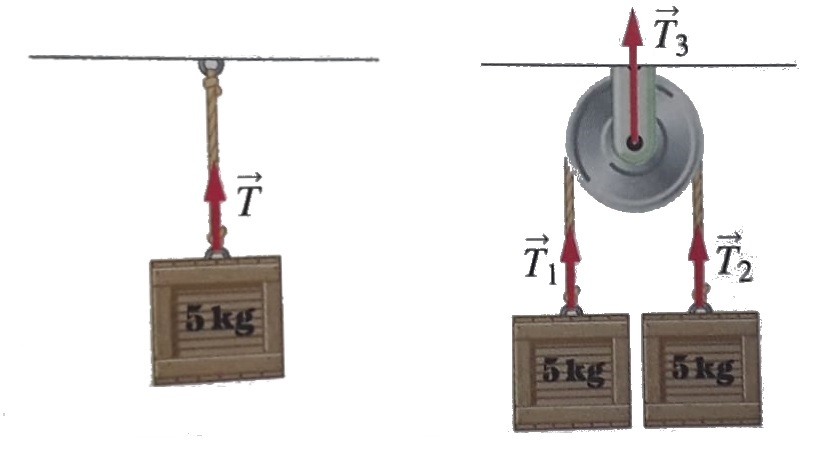
![]() , calcola la tensione della corda in condizioni di equilibrio e la reazione vincolare del soffitto.
, calcola la tensione della corda in condizioni di equilibrio e la reazione vincolare del soffitto.