Indice
Problema 1
Punto a
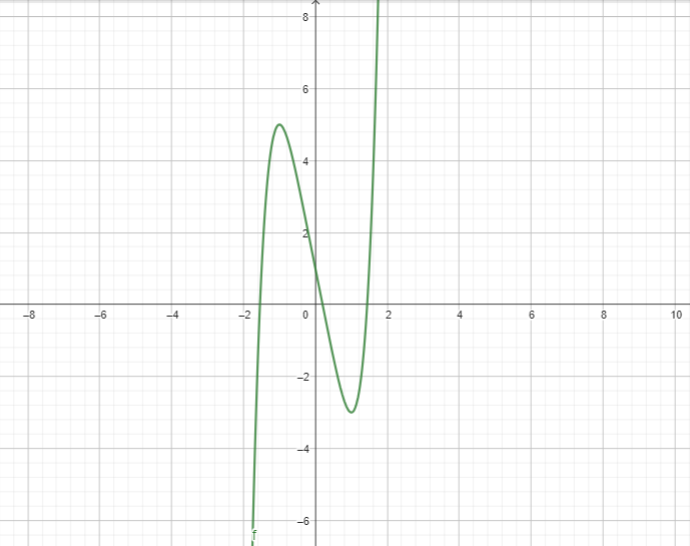
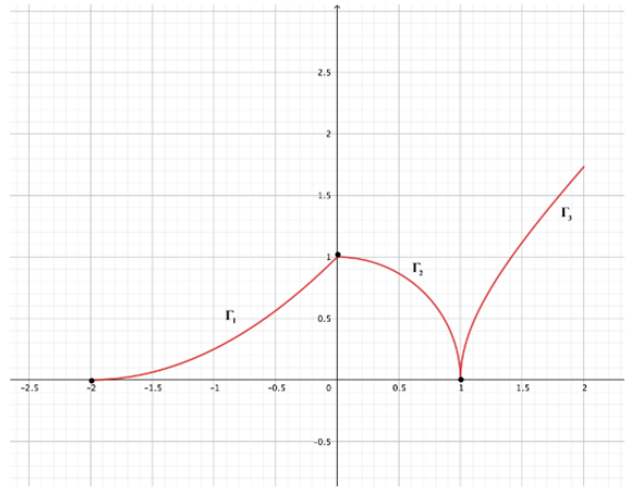
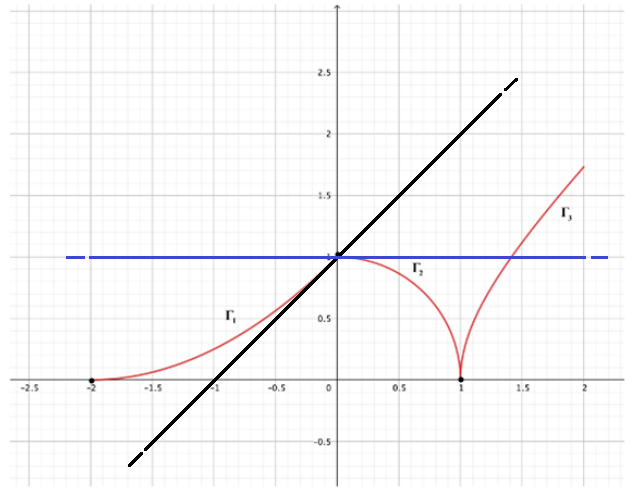
Dal grafico presente nel testo dell’esercizio possiamo dedurre i punti da cui passano i tre pezzi di grafico (la pratica di dedurre i punti dal grafico non è completamente corretta, sarebbe stato meglio che il ministero avesse esplicitato i punti). Possiamo quindi dedurre che
il grafico 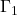 parta dal punto
parta dal punto 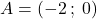 e arrivi al punto
e arrivi al punto 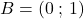 , che il grafico
, che il grafico 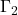 parta dal punto
parta dal punto 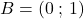 e arrivi al punto
e arrivi al punto 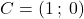 e infine che il grafico
e infine che il grafico 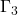 parta dal punto
parta dal punto 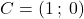 . Una volta dedotto questo, per ottenere l’espressione analitica della funzione nell’intervallo
. Una volta dedotto questo, per ottenere l’espressione analitica della funzione nell’intervallo ![Rendered by QuickLaTeX.com [-2\:;\:2]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-92fa93da90bb785874ed08e856db3088_l3.png) ci basta sostituire, quindi imponendo il passaggio di
ci basta sostituire, quindi imponendo il passaggio di 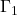 per
per 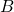 avremo che
avremo che
![Rendered by QuickLaTeX.com \[y=a(x+2)^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-f4d5ba9d60151d23c7b852a229944af0_l3.png)
![Rendered by QuickLaTeX.com \[1=a(0+2)^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-00f0f85b4b9f49e5382616d0f53e5971_l3.png)
![Rendered by QuickLaTeX.com \[1=4a\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-c33da6ee8a11e1d802b98a838dab6c5d_l3.png)
![Rendered by QuickLaTeX.com \[a={1\over 4}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-c1aebb8be7f634a30f58ba0b95149300_l3.png)
Imponendo il passaggio di
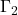
sempre per
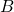
avremo che
![Rendered by QuickLaTeX.com \[x^2+y^2+b=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d8c52a277da40d7411047f4cba4c64f3_l3.png)
![Rendered by QuickLaTeX.com \[0^2+1^2+b=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-906689e45bf509bc6f6f99fd69f3401d_l3.png)
![Rendered by QuickLaTeX.com \[b=-1\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-b7208cf6ca54ba52540f26ece63ba54d_l3.png)
e infine imponendo il passaggio di
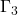
per
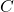
otteniamo
![Rendered by QuickLaTeX.com \[x^2-y^2+c=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-41327dd45d567534b33fe735718b577a_l3.png)
![Rendered by QuickLaTeX.com \[1^2+0^2+c=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-0fda238f54ff850bf6ddcc3b5c4af501_l3.png)
![Rendered by QuickLaTeX.com \[c=-1\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6d2b4266e2a8b8b23799119a0b6045f1_l3.png)
da cui avremo
![Rendered by QuickLaTeX.com \[\begin{cases} y={1\over 4}(x+2)^2\qquad &se\:\in [-2\:;\:0] \\ x^2+y^2-1=0\: &se\:\in [0\:;\:1]\\ x^2-y^2-1=0\: &se\:\in [1\:;\:2] \end{cases} \Rightarrow y=f(x)=\begin{cases} {1\over 4}(x+2)^2\qquad &se\:\in [-2\:;\:0] \\\sqrt{1-x^2}\: &se\:\in [0\:;\:1]\\ \sqrt{x^2-1}\: &se\:\in [1\:;\:2] \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8660f97e25bc481afaff9219f3bae5bf_l3.png)
Una volta dedotta la forma analitica della funzione possiamo osservare che all’interno dei tre intervalli
![Rendered by QuickLaTeX.com [-2\:;\:0]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8a7aa4e5b295b03e2d1d34fa3f30318c_l3.png)
,
![Rendered by QuickLaTeX.com [0\:;\:1]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6939875d583c859fded7d7a9a8cb8e0c_l3.png)
e
![Rendered by QuickLaTeX.com [1\:;\:2]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-37e741d9e25a7222f2631d2ec6c6d9dc_l3.png)
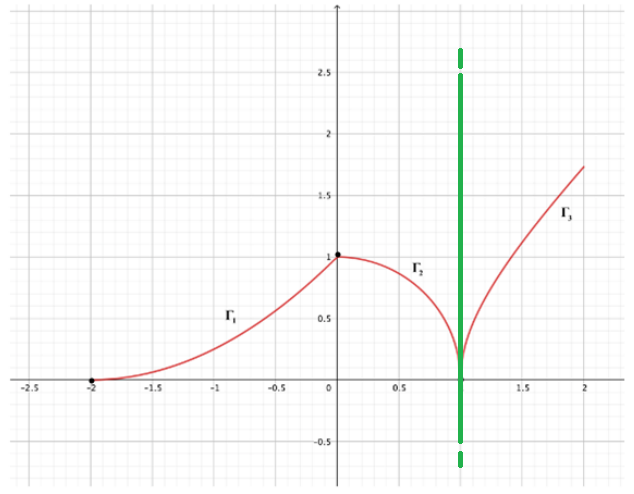
la funzione è sicuramente derivabile (questo perchè le funzioni definite nei singoli intervalli sappiamo essere derivabili), ci rimangono solo dei dubbi sui due punti di ascissa
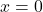
e
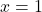
. Prima di procedere analiticamente con il calcolo ragioniamo sul concetto di derivata. Sappiamo che la derivata è il coefficiente angolare della retta tangente al grafico e sappiamo che questo coefficiente angolare deve essere un numero finito affinché la funzione sia derivabile. Pertanto in entrambi i punti la funzione non sarà derivabile, infatti nel punto di ascissa
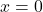
la retta tangente che si ottiene percorrendo il grafico
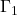
verso destra (retta nera) è diversa dalla retta tangente che si ottiene percorrendo il grafico
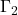
verso sinistra (retta blu) e quindi il punto è un punto angoloso
mentre il punto di ascissa 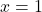 possiede la retta tangente parallela all’asse
possiede la retta tangente parallela all’asse 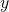 (retta verde) e quindi è un punto di cuspide
(retta verde) e quindi è un punto di cuspide
Una volta fatto questo ragionamento intuitivo supportiamo tale ragionamento attraverso i calcoli analitici delle derivate. Allora
![Rendered by QuickLaTeX.com \[f'(x)=\begin{cases} {1\over 4}\cdot 2\cdot (x+2)={1\over 2}(x+2)\qquad &se\:\in [-2\:;\:0] \\\\{1\over 2}(1-x^2)^{-1/2}\cdot(-2x)={-x\over \sqrt{1-x^2}}\: &se\:\in [0\:;\:1]\\ \\{1\over 2}(x^2-1)^{-1/2}\cdot(2x)={x\over \sqrt{x^2-1}}\: &se\:\in [1\:;\:2] \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-fb79aeb788e9ef96ef24b1b58577c04e_l3.png)
Da cui è possibile vedere che le due derivate calcolate nel punto
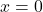
sono diverse a seconda di che espressione consideriamo e che la derivata nel punto
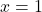
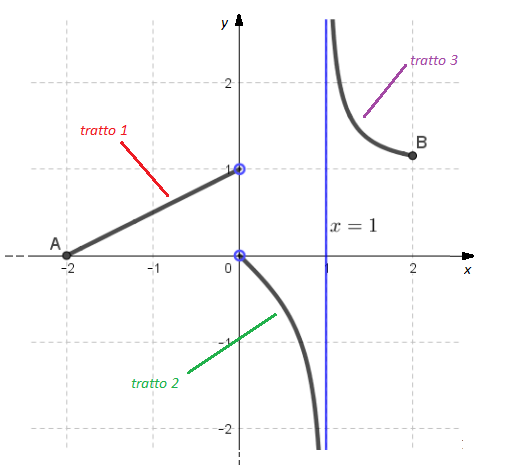
ha valore non finito. A questo punto completiamo il punto a) del problema calcolando la derivata nei punti di ascissa
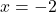
,
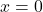
,
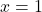
e
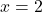
. La retta tangente al punto di ascissa
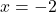
è la retta che passa per
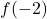
e ha come coefficiente angolare
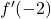
(questo vale per ogni punto di derivabilità della funzione e quindi anche per
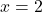
, mentre per gli altri due punti dovremo fare due discorsi differenti). Pertanto, siccome
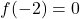
e
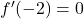
, la retta tangente al grafico nel punto di ascissa
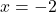
è
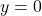
che è esattamente l’asse
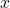
. La retta tangente al punto
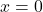
, come abbiamo già ampiamente detto, non esiste. La retta tangente al punto di ascissa
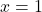
(la retta verde del grafico precedente) è la retta
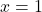
. Infine la retta tangente al grafico nel punto
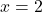
, siccome
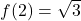
e
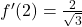
, ha equazione
![Rendered by QuickLaTeX.com \[y-\sqrt3={2\over \sqrt 3}\cdot (x-2)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-f8b2761bcef669f23cf7293c7f3d57e3_l3.png)
![Rendered by QuickLaTeX.com \[y={2\over \sqrt 3}x-{4\over \sqrt 3}+\sqrt 3\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-b7e5f639ce29c9bbfd2929e7d2e9885a_l3.png)
![Rendered by QuickLaTeX.com \[y={2\over \sqrt 3}x+{-4+3\over \sqrt 3}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-dd41e6f7b7142ff592f3a7cf9db17e4a_l3.png)
![Rendered by QuickLaTeX.com \[y={2\over \sqrt 3}x-{1\over \sqrt 3}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-dee01398731914751276e8a312f13859_l3.png)
Ritorna all’indice
Punto b
Per rispondere al punto b) osserviamo che dobbiamo dedurre il grafico della derivata a partire dal grafico della funzione 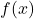 , non dobbiamo semplicemente dedurre il grafico di
, non dobbiamo semplicemente dedurre il grafico di 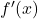 partendo dalla sua espressione analitica (trovata nel punto a)). Nel primo tratto (quello relativo alla parabola) la derivata parte da un valore uguale a
partendo dalla sua espressione analitica (trovata nel punto a)). Nel primo tratto (quello relativo alla parabola) la derivata parte da un valore uguale a 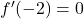 e tende a
e tende a 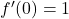 (infatti abbiamo già detto nel punto
(infatti abbiamo già detto nel punto 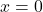 la derivata non c’è, nonostante questo da sinistra la derivata tende ad essere
la derivata non c’è, nonostante questo da sinistra la derivata tende ad essere 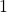 ). Nel secondo tratto (quello relativo alla circonferenza) la derivata parte da
). Nel secondo tratto (quello relativo alla circonferenza) la derivata parte da 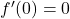 (ancora una volta il valore
(ancora una volta il valore 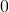 non è considerato) e tende ad arrivare a
non è considerato) e tende ad arrivare a  (infatti la tangente tende alla retta
(infatti la tangente tende alla retta 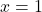 ). Superato il punto
). Superato il punto 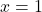 e arrivati all’ultimo tratto (quello relativo al’arco di iperbole) si ha che la derivata parte da
e arrivati all’ultimo tratto (quello relativo al’arco di iperbole) si ha che la derivata parte da 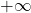 fino ad arrivare a
fino ad arrivare a 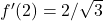 . In definitiva il grafico sarà qualcosa del tipo
. In definitiva il grafico sarà qualcosa del tipo
Cerchiamo ora di studiare la funzione integrale
![Rendered by QuickLaTeX.com \[F(x)=\int_{-2}^{x}f(t)dt\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-0d469b76e4cc85e36a40caccb2310026_l3.png)
siccome
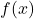
è continua nell’intervallo
![Rendered by QuickLaTeX.com [-2\:;\:2]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-92fa93da90bb785874ed08e856db3088_l3.png)
la prima parte del teorema fondamentale del calcolo integrale ci dice che
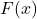
è derivabile, inoltre
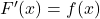
e quindi
![Rendered by QuickLaTeX.com \[F''(x)=f'(x)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-7fcb8fef6f0eed32a432ed8c58b2e7bb_l3.png)
pertanto per studiare la concavità e la convessità della funzione integrale ci basta studiare il grafico di
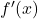
(che abbiamo appena dedotto). Per cui la funzione
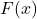
sarà convessa negli intervalli in cui
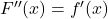
è positiva, ossia
![Rendered by QuickLaTeX.com ]-2\:;\:0[](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-27c6520e500d12b3c7510c951e9b6df4_l3.png)
e
![Rendered by QuickLaTeX.com ]1\:;\: 2[](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d28f2dd2a3a886cc20fd7298d7996209_l3.png)
, e sarà concava negli intervalli in cui la derivata seconda è negativa, ossia
![Rendered by QuickLaTeX.com ]0\:;\:1[](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-783e22cdb22e3c3b8d0e1837348512aa_l3.png)
.
Ritorna all’indice
Punto c
La funzione
![Rendered by QuickLaTeX.com \[y={1\over 4}(x+2)^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9eb2e849c44bff3cbbb7bb11df657e7a_l3.png)
definita sull’intervallo
![Rendered by QuickLaTeX.com [-2\:;\:0]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8a7aa4e5b295b03e2d1d34fa3f30318c_l3.png)
è una funzione continua e strettamente crescente (possiamo vederlo graficamente oppure in maniera più precisa andando ad esaminare la derivata calcolata in precedenza che è sempre strettamente positiva tranne nel punto
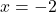
) pertanto sappiamo essere invertibile. Per calcolare la sua inversa ci basta determinare
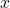
in funzione di
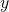
, da cui
![Rendered by QuickLaTeX.com \[y={1\over 4}(x+2)^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9eb2e849c44bff3cbbb7bb11df657e7a_l3.png)
![Rendered by QuickLaTeX.com \[4y=(x+2)^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9ba658717e070a23825023152da78db8_l3.png)
![Rendered by QuickLaTeX.com \[\sqrt{4y}=x+2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-95eb802728463b973e2671a22b5300dc_l3.png)
![Rendered by QuickLaTeX.com \[x=\sqrt{4y}-2=2\sqrt y-2=2(\sqrt y-1)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8d712655c2fdadd757555229b8d59b03_l3.png)
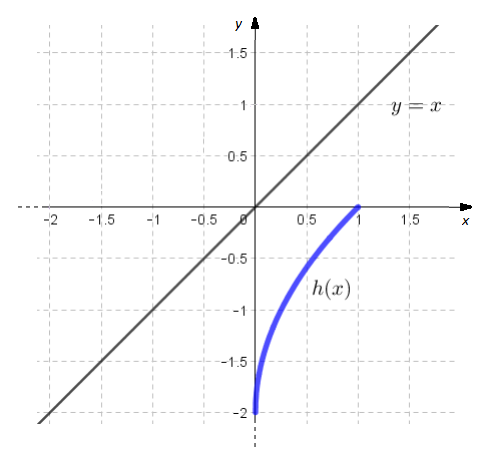
Pertanto la funzione
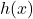
(quindi scritta cambiando il nome delle variabili) sarà
![Rendered by QuickLaTeX.com \[h(x)=2(\sqrt x-1)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-7a86dbb98afe46434bf25f1cf90ed3f7_l3.png)
che è una funzione derivabile nel suo dominio naturale
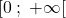
e la cui derivata è
![Rendered by QuickLaTeX.com \[h'(x)=2\cdot {1\over 2}\cdot {1\over \sqrt x}={1\over \sqrt x}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9eaf6bfd5b49c5542568ac547abe5967_l3.png)
perfettamente definita nell’intervallo
![Rendered by QuickLaTeX.com ]0\:;\:+\infty[](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-cfa79a32ab6dcd5400e707b7a8929e49_l3.png)
. Infine per disegnarne il grafico osserviamo che
![Rendered by QuickLaTeX.com \[y=2(\sqrt x-1)\Rightarrow x={1\over 4}(y+2)^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-986a7d032de33892a987e7c0674d2cf6_l3.png)
pertanto il grafico di
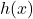
è uguale al grafico di
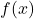
in
![Rendered by QuickLaTeX.com [-2\:;\:0]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8a7aa4e5b295b03e2d1d34fa3f30318c_l3.png)
dove abbiamo invertito gli assi cartesiani (quindi sono speculari rispetto alla bisettrice del primo e terzo quadrante
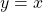
), da cui
Dove abbiamo rappresentato solo la funzione 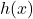 inversa dell’arco di parabola di
inversa dell’arco di parabola di 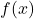 .
.
Ritorna all’indice
Punto d
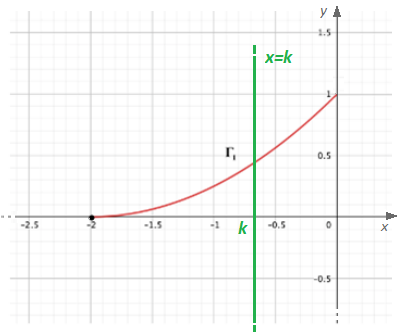
Risolviamo infine l’ultimo punto del primo problema. Cerchiamo di capire a livello grafico quello che dobbiamo fare: dobbiamo trovare la costante 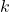 per cui la retta
per cui la retta 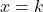 (retta verde) divide in due parti di equale area il sottografico di
(retta verde) divide in due parti di equale area il sottografico di 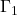
Quindi prima di tutto calcoliamo l’area del sottografico di 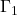 e poi imponiamo che l’area del sottografico di
e poi imponiamo che l’area del sottografico di 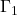 fino a
fino a 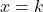 sia esattamente la sua metà. Per fare questo utilizziamo il calcolo integrale (nonostante si possano usare anche le nozioni di geometria analitica imparate in terza per l’area del segmento parabolico). Allora
sia esattamente la sua metà. Per fare questo utilizziamo il calcolo integrale (nonostante si possano usare anche le nozioni di geometria analitica imparate in terza per l’area del segmento parabolico). Allora
![Rendered by QuickLaTeX.com \[A_{\Gamma_1}^{[-2\:;\:0]}=\int_{-2}^{0}{1\over 4}(x+2)^2dx={1\over 4}\cdot\Big[{1\over 3}(x+2)^3\Big]_{-2}^0={2\over 3}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-44051bd0aee1095608edc9e8d9810966_l3.png)
da cui
![Rendered by QuickLaTeX.com \[A_{\Gamma_1}^{[-2\:;\:k]}={1\over 3}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-64513a4993ede7d148dbf76af2425446_l3.png)
![Rendered by QuickLaTeX.com \[\int_{-2}^{k}{1\over 4}(x+2)^2dx={1\over 3}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-91b7fa805e3c3e80b3ce4c9c41f9a8d1_l3.png)
![Rendered by QuickLaTeX.com \[{1\over 4}\cdot\Big[{1\over 3}(x+2)^3\Big]_{-2}^0={1\over 3}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-952a5c180fa64b5ca15f66869fa7811d_l3.png)
![Rendered by QuickLaTeX.com \[{1\over 12}(k+2)^3={1\over 3}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-a8f38ef73d3b697e2a52cc8d97294bd9_l3.png)
![Rendered by QuickLaTeX.com \[(k+2)^3=4\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-e5df20d5c114cf618594bb5315a696f0_l3.png)
![Rendered by QuickLaTeX.com \[k+2=\sqrt[3]4\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-ca2457137ba834e20b501e4e9a6bd3be_l3.png)
![Rendered by QuickLaTeX.com \[k=\sqrt[3]4-2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-fa0c4749f6bedd5b8937f13afcc78c2f_l3.png)
Ritorna all’indice
Problema 2
Punto a
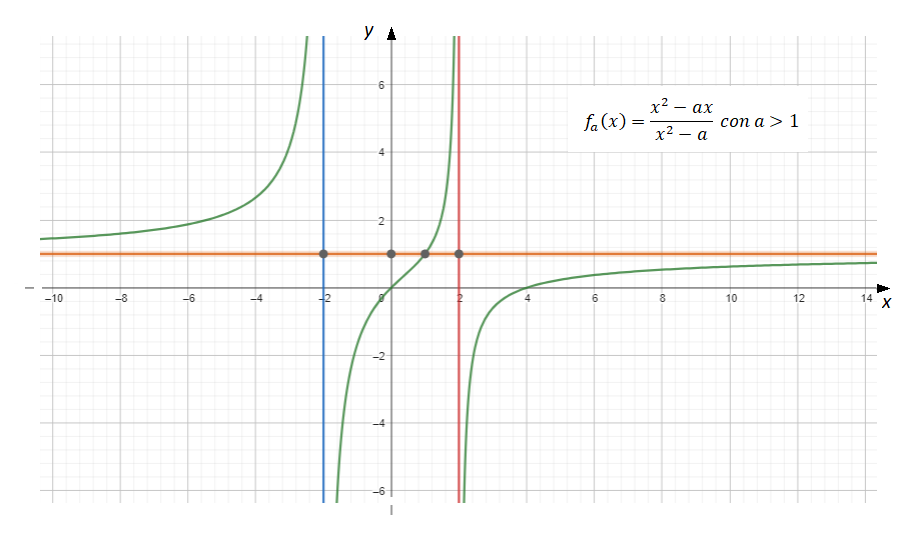
Studiando, al variare di 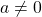 , la funzione
, la funzione
![Rendered by QuickLaTeX.com \[f_a(x)={x^2-ax\over x^2-a}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-43b40b3ce75f7185c0639430cfc264b1_l3.png)
possiamo subito notare che il numeratore e il denominatore sono continui nel loro dominio naturale e che l’unico “problema” potrebbe essere rappresentato dal denominatore che dovrà essere sempre diverso da zero per dare senso alla divisione. Fatta questa premessa risulta evidente che se fosse
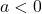
allora
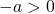
per cui
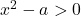
e quindi la funzione sarebbe continua in tutto
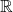
. Nel caso in cui
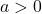
dobbiamo imporre che il denominatore sia sempre diverso da zero, cioè
![Rendered by QuickLaTeX.com \[x^2-a\neq 0\Rightarrow x\neq \pm\sqrt a\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-57f9d43b51491470504d132ce117643e_l3.png)
quindi abbiamo due punti di discontinuità in
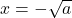
e
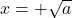
. Per studiare che punti di discontinuità sono e i vari asintoti utilizziamo i limiti. Per
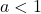
, siccome non abbiamo punti di discontinuità all’interno di
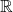
, potremmo avere solo asintoti orizzontali o obliqui, pertanto studiamo
![Rendered by QuickLaTeX.com \[\lim_{x\to -\infty}f(x)=\lim_{x\to -\infty}{x^2-ax\over x^2-a}=1\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-723c56a6817acf2c7cded85481e8229b_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x\to +\infty}f(x)=\lim_{x\to +\infty}{x^2-ax\over x^2-a}=1\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-7e9fcf39bc0b9333de5d7ef9dad9b53e_l3.png)
e questo a prescindere dal valore di
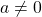
. Pertanto in ogni caso la funzione
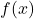
presenta l’asintoto orizzontale
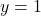
. Studiamo ora i limiti per
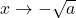
e per
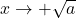
nel caso in cui
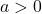
. Allora se
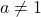
![Rendered by QuickLaTeX.com \[\lim_{x\to -\sqrt a^-}f(x)=\lim_{x\to -\sqrt a^-}{x^2-ax\over x^2-a}=+\infty\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-2fcbe48725ac74346285a203678d59b2_l3.png)
a prescindere dal valore di
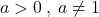
in quanto il numeratore è sempre un numero positivo diverso da zero e il denominatore tende a
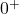
. Un discorso analogo lo possiamo fare per
![Rendered by QuickLaTeX.com \[\lim_{x\to -\sqrt a^+}f(x)=\lim_{x\to -\sqrt a^+}{x^2-ax\over x^2-a}=-\infty\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-98369b12e3f17f1c535f199565782a55_l3.png)
dove osserviamo esplicitamente che tutto questo è così perchè se
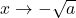
il numeratore
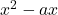
tende sicuramente a qualcosa di positivo. Discorso diverso abbiamo nel limite per
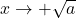
, infatti in questo caso il numeratore sarà una volta positivo e una volta negativo. In particolare
![Rendered by QuickLaTeX.com \[\lim_{x\to +\sqrt a^-}f(x)=\lim_{x\to +\sqrt a^-}{x^2-ax\over x^2-a}=\pm\infty\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-04cd7a0545dde79d196da454c7b32bb4_l3.png)
infatti il denominatore tende sempre a
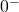
a prescindere dal valore di

, mentre il numeratore tende ad essere un numero positivo se
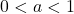
e negativo se
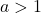
. Pertanto tale limite sarà

se
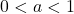
e
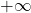
se
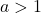
. Discorso del tutto analogo (ma al contrario con i segni) possiamo farlo per
![Rendered by QuickLaTeX.com \[\lim_{x\to +\sqrt a^+}f(x)=\lim_{x\to +\sqrt a^+}{x^2-ax\over x^2-a}=\mp\infty\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d58719383ca0e88625adf00a34bfbb95_l3.png)
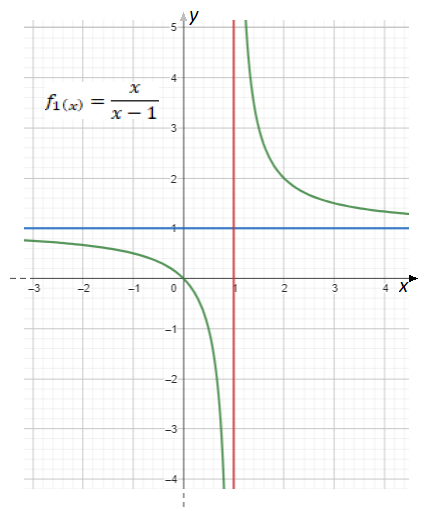
Da questa discussione con i limiti viene fuori che il caso
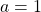
comporta delle leggere differenze, infatti a uno studio un attimo più approfondito si nota che quando
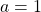
allora
![Rendered by QuickLaTeX.com \[f_1(x)={x^2-x\over x^2-1}={x\cdot (x+1)\over (x+1)\cdot (x-1)}={x\over x-1}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-31a198dbcca1aa0ce01cdc23ddd125da_l3.png)
che quindi ha dominio
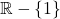
e
![Rendered by QuickLaTeX.com \[\lim_{x\to 1}f_1(x)=\lim_{x\to 1}{{x\over x-1}}=\mp\infty\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-a5f315e4445b8f9cc37a07c9e24e91d2_l3.png)
negativo se
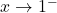
positivo se
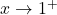
. Ricapitolando abbiamo tutti punto di discontinuità di seconda specie e come asintoti quello orizzontale
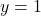
per ogni
, quelli verticali
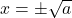
per ogni
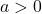
e
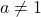
e invece per
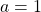
quello verticale
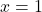
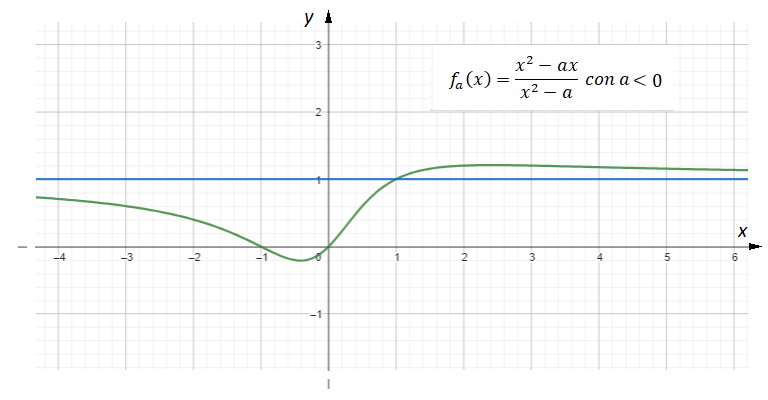
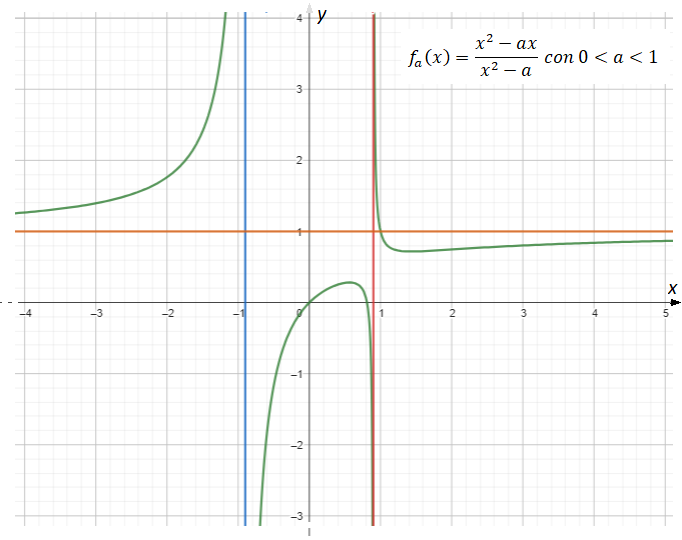
. Nel dettaglio le quattro tipologie di grafico di
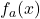
sono
Ritorna all’indice
Punto b
Le intersezioni tra 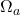 e il suo asintoto orizzontale sono le soluzione del sistema
e il suo asintoto orizzontale sono le soluzione del sistema
![Rendered by QuickLaTeX.com \[\begin{cases} y={x^2-ax\over x^2-a} \\\\y=1 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-0a586ff7031e7d510f311c52062d8969_l3.png)
che è facilmente risolvile per sostituzione
![Rendered by QuickLaTeX.com \[\begin{cases} y={x^2-ax\over x^2-a} \\y=1 \end{cases}=\begin{cases} 1={x^2-ax\over x^2-a} \\y=1 \end{cases}=\begin{cases} x^2-a=x^2-ax \\y=1 \end{cases}=\begin{cases} -a=-ax \\y=1 \end{cases}=\begin{cases} x=1\\y=1 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9f998607394a92f186299806882a2134_l3.png)
quindi la soluzione è indipendente dal parametro

. Osserviamo anche esplicitamente che tale soluzione per
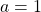
non la possiamo accettare (nonostante quel sistema sia comunque risolvibile nello stesso identico modo) perchè il dominio di
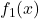
non contiene il punto
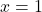
. Per rispondere al secondo punto facciamo vedere che
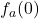
e
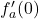
sono indipendenti dal parametro

qualunque
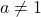
si consideri. Infatti
![Rendered by QuickLaTeX.com \[f_a(0)={0^2-a\cdot 0\over 0-a}=-{0\over a}=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-2eda10d4383bce501cae2bcc22418907_l3.png)
Invece
![Rendered by QuickLaTeX.com \[f'_a(x)={(2x-a)(x^2-a)-(x^2-ax)\cdot 2x\over (x^2-a)^2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-fbc78c1b086072d2c32c8fe33e341e70_l3.png)
![Rendered by QuickLaTeX.com \[f'_a(x)={2x^3-2ax-ax^2+a^2-2x^3+2ax^2\over (x^2-a)^2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-5214f1f17144da8e3d70147c4e5e7cb9_l3.png)
![Rendered by QuickLaTeX.com \[f'_a(x)={ax^2-2ax+a^2\over (x^2-a)^2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-ffc7e6ef76eebd00d1294527b993ca10_l3.png)
pertanto
![Rendered by QuickLaTeX.com \[f'_a(0)=1\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-119e86246e79bdababeaa1a487bf6fb2_l3.png)
qualunque sia il parametro
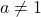
.
Ritorna all’indice
Punto c
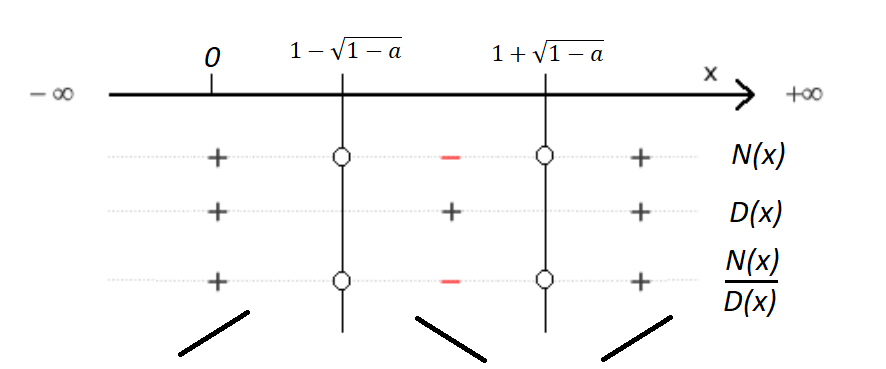
Per studiare la monotonia di una funzione dobbiamo studiare il segno della derivata prima di tale funzione. Dal punto a) sappiamo che
![Rendered by QuickLaTeX.com \[f'_a(x)={ax^2-2ax+a^2\over (x^2-a)^2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-ffc7e6ef76eebd00d1294527b993ca10_l3.png)
pertanto il denominatore è sempre positivo e il segno della derivata dipende esclusivamente dal segno del numeratore. Il numeratore è una parabola che tocca l’asse
nei punti che verificano l’equazione associata
![Rendered by QuickLaTeX.com \[ax^2-2ax+a^2=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d7936e6152f80a9d9d12281c59e55447_l3.png)
quindi
![Rendered by QuickLaTeX.com \[\Delta=4a^2-4a^3=4a^2\cdot(1-a)>0\:quando\:a\neq 0\:e\:a<1\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8152a1cc509fdada4be5f9d798e8ff0d_l3.png)
![Rendered by QuickLaTeX.com \[x_{1,2}={2a\pm\sqrt{4a^2\cdot(1-a)}\over 2a}={2a\pm 2a\cdot\sqrt{1-a}\over 2a}=1\pm\sqrt{1-a}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8ad78ac1a20bc10c0a5f48a6cd12e211_l3.png)
e siccome quando
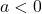
la parabola ha concavità rivolta verso il basso sappiamo che sarà negativa esternamente e positiva internamente e quindi il segno della derivata sarà
mentre quando 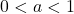 la parabola avrà concavità rivolta verso l’alto e quindi il suo segno sarà
la parabola avrà concavità rivolta verso l’alto e quindi il suo segno sarà
Notiamo anche esplicitamente che questi segni sono il linea con i grafici che abbiamo ottenuto nel punto a).
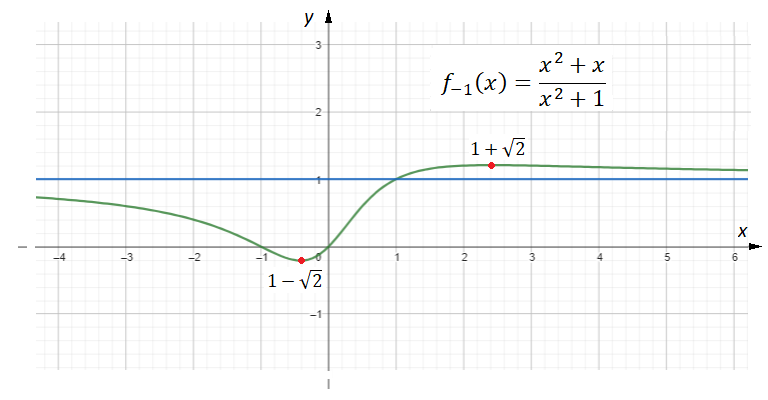
Per completare il punto c) studiamo la funzione che si ottiene quando 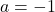 , ossia
, ossia
![Rendered by QuickLaTeX.com \[f_{-1}(x)={x^2+x\over x^2+1}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-f3a048f8dfedd7bb0fc9cf3cae1d6e3b_l3.png)
osserviamo che sappiamo già tutto di questa funzione, infatti nei punti precedenti ne abbiamo studiato il dominio, i limiti, la monotonia e i punti di massimo e minimo (deducibili dal grafico dei segni scritto sopra), pertanto possiamo concludere che il grafico
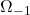
sarà
Ritorna all’indice
Punto d
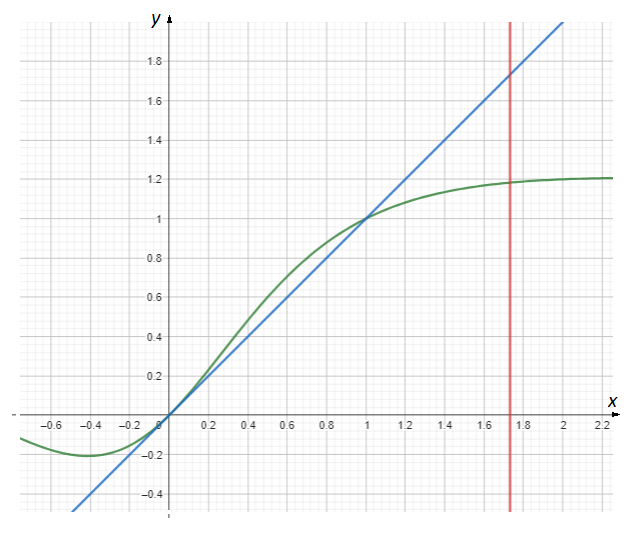
Per risolvere questo ultimo punto è necessario prima di tutto capire perfettamente quale area ci viene richiesto di calcolare, pertanto preliminarmente calcoliamo la tangente al grafico nell’origine e vediamo come è posizionata rispetto al grafico 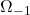 . Dal punto b) dell’esercizio sappiamo che la retta tangente è la bisettrice del primo e terzo quadrante, ossia
. Dal punto b) dell’esercizio sappiamo che la retta tangente è la bisettrice del primo e terzo quadrante, ossia 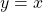 e questa retta interseca il grafico nei due punti
e questa retta interseca il grafico nei due punti 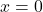 e
e 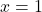 , infatti queste sono le soluzioni del seguente sistema
, infatti queste sono le soluzioni del seguente sistema
![Rendered by QuickLaTeX.com \[\begin{cases} y={x^2+x\over x^2+1} \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-5a3d996f86c75cff28c2a1ac25a26360_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x={x^2+x\over x^2+1} \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-cc78f07fc5fbb1320a837c4c3a116852_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} (x^2+1)\cdot x=x^2+x \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-1d3a7c020d979c3e5d0be621ed4deb58_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^3+x=x^2+x \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-e83e57e67c9d0464bc22c1e67b3f10fb_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^3-x^2=0 \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-42b2d48e4880b50fb49d1f6df0c32136_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2\cdot (x-1)=0 \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6b492800f97dcd9e2f610ab2c8ac2c9d_l3.png)
Per concludere la nostra idea dell’area da calcolare (necessaria per imbastire correttamente l’integrale che ci permetterà di completare il calcolo) cerchiamo di capire se la retta è minore o maggiore di
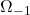
. Per fare questo studiamo il segno della seguente funzione
![Rendered by QuickLaTeX.com \[{x^2+x\over x^2+1}-x\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-caaf017ca51cf9b74081476990d38394_l3.png)
che è la sottrazione tra la funzione
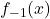
e la retta. Pertanto
![Rendered by QuickLaTeX.com \[{x^2+x\over x^2+1}-x>0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-7dffc92489e0dbd0e3dfffc99eca5a11_l3.png)
![Rendered by QuickLaTeX.com \[{x^2+x-x^3-x\over x^2+1}>0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6e6a838796681df3393964a3898a1135_l3.png)
![Rendered by QuickLaTeX.com \[{x^2-x^3\over x^2+1}>0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-fffe6c8be464842bd6472edde2879817_l3.png)
![Rendered by QuickLaTeX.com \[{x^2\cdot (1-x)\over x^2+1}>0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-da754b25c2613bb4c36d4461fb38d0b0_l3.png)
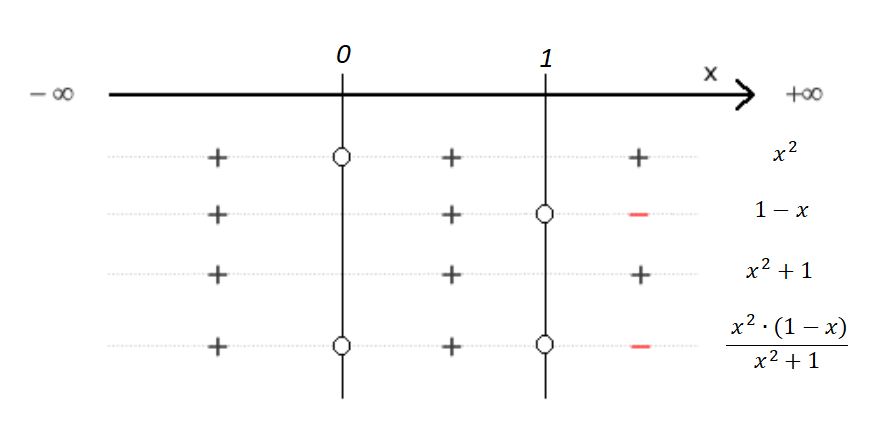
e quindi per studiare il segno complessivo della frazione studiamo il segno dei tre “blocchi” separatamente. Sappiamo che
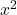
e
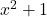
sono sempre positivi, mentre
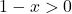
se
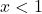
, per cui lo schema dei segni sarà
Da cui possiamo dedurre che il grafico 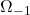 sta “sopra” la retta tra
sta “sopra” la retta tra 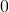 e
e 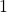 e “sotto” tra
e “sotto” tra 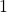 e
e 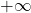 . La situazione sarà qualcosa del tipo
. La situazione sarà qualcosa del tipo
Per calcolare l’area compresa tra le rette blu, rosse e il grafico verde impostiamo il seguente calcolo integrale
![Rendered by QuickLaTeX.com \[\int_{1}^{\sqrt{3}}xdx-\int_{1}^{\sqrt{3}}{x^2+x\over x^2+1}dx\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-323f8778d72b89d5a3d7968d3a30c684_l3.png)
![Rendered by QuickLaTeX.com \[\int_{1}^{\sqrt{3}}xdx-\int_{1}^{\sqrt{3}}{x^2+1-1+x\over x^2+1}dx\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-a5bce92f6877096a0fd668e2975952b0_l3.png)
![Rendered by QuickLaTeX.com \[\int_{1}^{\sqrt{3}}xdx-\int_{1}^{\sqrt{3}}{x^2+1\over x^2+1}+{-1+x\over x^2+1}dx\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-edb1ef950a09fbf00d9a1f3d0a39ae02_l3.png)
![Rendered by QuickLaTeX.com \[\int_{1}^{\sqrt{3}}xdx-\int_{1}^{\sqrt{3}}1+{x\over x^2+1 }-{1\over x^2+1}dx\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-74f98f22c503331bff13c1d5b2d125b8_l3.png)
![Rendered by QuickLaTeX.com \[\int_{1}^{\sqrt{3}}xdx-\int_{1}^{\sqrt{3}}1dx-\int_{1}^{\sqrt{3}}{x\over x^2+1}dx+\int_{1}^{\sqrt{3}}{1\over x^2+1}dx\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-bb86aa412f692fcb4dd5027c84f1d81b_l3.png)
![Rendered by QuickLaTeX.com \[\Big[ {x^2\over 2}\Big]_{1}^{\sqrt{3}}-\Big[x \Big]_{1}^{\sqrt{3}}-\Big[{1\over 2 }\ln(x^2+1) \Big]_{1}^{\sqrt{3}}+\Big[\arctan(x) \Big]_{1}^{\sqrt{3}}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-272860bd61af5b6bb5c19d7e7d795ca7_l3.png)
![Rendered by QuickLaTeX.com \[({3\over 2}-{1\over 2})-(\sqrt 3-1)-({1\over 2}\cdot \ln(4)-{1\over 2}\cdot \ln(2))+(\arctan(\sqrt 3)-\arctan(1))\approx 0,18\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9c202ea549032966156e32c4738cf29c_l3.png)
Ritorna all’indice
Quesito 1
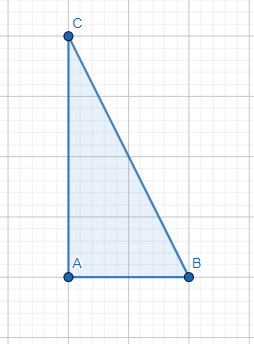
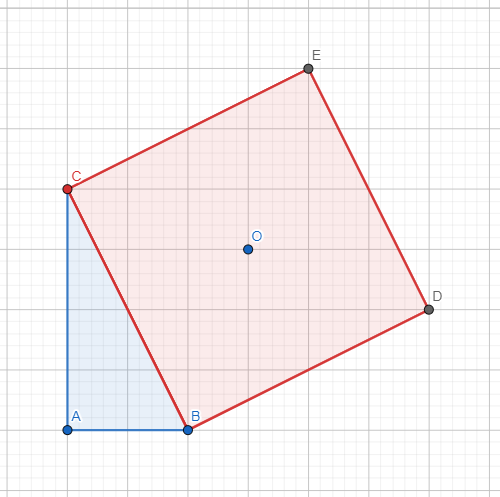
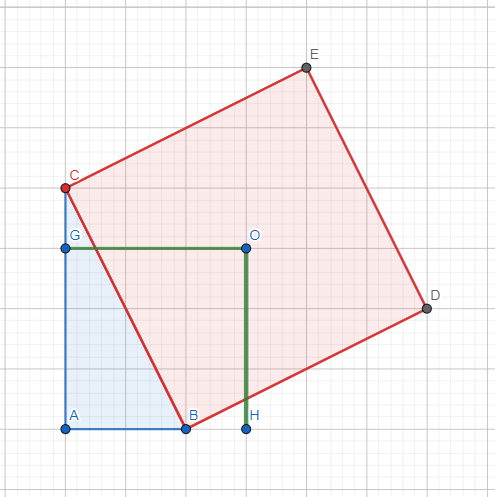
Prima di tutto costruiamo la figura passo passo. Quindi tracciamo il triangolo rettangolo
Tracciamo il quadrato di lato 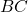
e infine tracciamo le due distanze che dobbiamo dimostrare essere congruenti
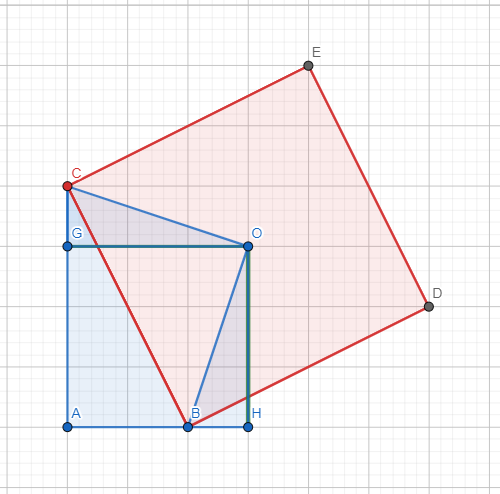
A questo punto procediamo con la dimostrazione. L’idea è quella di dimostrare che i due triangoli 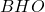 e
e 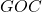 sono congruenti
sono congruenti
Sicuramente, per definizione di distanza, sono due triangoli rettangoli, inoltre il lato 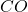 e il lato
e il lato 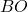 sono congruenti in quanto mezza diagonale del quadrato. A questo punto se dimostriamo che gli angoli sono congruenti abbiamo terminato. Ma questo è relativamente facile da vedere, infatti l’angolo
sono congruenti in quanto mezza diagonale del quadrato. A questo punto se dimostriamo che gli angoli sono congruenti abbiamo terminato. Ma questo è relativamente facile da vedere, infatti l’angolo 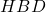 e l’angolo
e l’angolo 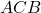 sono congruenti perchè entrambi sono calcolabili con la formula
sono congruenti perchè entrambi sono calcolabili con la formula 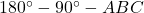 mentre gli angoli
mentre gli angoli 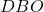 e
e 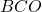 sono congruenti (e pari a
sono congruenti (e pari a 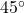 ) in quanto la diagonale del quadrato è anche bisettrice degli angoli interni. Pertanto
) in quanto la diagonale del quadrato è anche bisettrice degli angoli interni. Pertanto 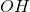 è congruente a
è congruente a 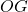 .
.
Ritorna all’indice
Quesito 2
Come primo passo dobbiamo determinare le probabilità 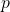 e
e 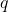 che esca un numero pari e che esca un numero dispari. Sicuramente dal testo dell’esercizio sappiamo che
che esca un numero pari e che esca un numero dispari. Sicuramente dal testo dell’esercizio sappiamo che 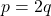 . Inoltre, dalle definizioni classiche di probabilità, sappiamo che la somma delle probabilità di tutti gli eventi elementari deve essere
. Inoltre, dalle definizioni classiche di probabilità, sappiamo che la somma delle probabilità di tutti gli eventi elementari deve essere 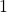 , ossia
, ossia 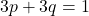 . Pertanto risolvendo il sistema
. Pertanto risolvendo il sistema
![Rendered by QuickLaTeX.com \[\begin{cases} p&=2q \\3p+3q&=1 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9723a37d0a3b74d0ef85be2545e8eced_l3.png)
si ottengono facilmente i valori di
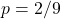
e
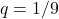
. Una volta ottenute le due probabilità cercate ragioniamo sugli eventi proposti dal testo dell’esercizio. La probabilità che esca un numero primo è uguale alla probabilità che esca un numero tra
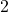
,
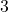
e
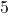
, per cui
![Rendered by QuickLaTeX.com \[P(primo)=P(2)+P(3)+P(5)={2\over 9}+{1\over 9}+{1\over 9}={4\over 9}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-92bc1d3be39e4953938072f5e9a0df8c_l3.png)
La probabilità che esca un numero almeno pari a
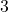
è uguale alla probabilità che esca un numero tra
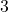
,
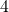
,
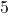
e
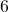
, per cui
![Rendered by QuickLaTeX.com \[P(almeno\:3)=P(3)+P(4)+P(5)+P(6)={1\over 9}+{2\over 9}+{1\over 9}+{2\over 9}={6\over 9}={2\over 3}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-f0175713c2fa0c76eeb6070d1d629a73_l3.png)
La probabilità che esca un numero al più pari a
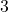
è uguale alla probabilità che esca un numero tra
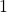
,
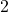
e
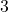
, per cui
![Rendered by QuickLaTeX.com \[P(al\:più\:3)=P(1)+P(2)+P(3)={1\over 9}+{2\over 9}+{1\over 9}={4\over 9}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8c19a66479806326cb4022d4e4d5cab6_l3.png)
Ritorna all’indice
Quesito 3
Risolviamo il quesito come se fosse un problema di geometria analitica di terza, quindi per prima cosa determiniamo l’equazione della retta passante per 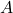 e
e 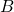 e in seguito cerchiamo, tra tutte le sfere di centro
e in seguito cerchiamo, tra tutte le sfere di centro 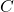 , l’unica che interseca la retta in un unico punto. Sappiamo che i punti che appartengono alla retta passante per
, l’unica che interseca la retta in un unico punto. Sappiamo che i punti che appartengono alla retta passante per 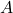 e
e 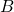 sono i punti che si possono ottenere partendo dal punto
sono i punti che si possono ottenere partendo dal punto 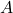 aggiungendo un vettore
aggiungendo un vettore 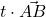 (equazione parametriche delle rette)
(equazione parametriche delle rette)
![Rendered by QuickLaTeX.com \[(x\:;\:y\:;\:z)=(x_A\:;\:y_A\:;\:z_A)+t\cdot (x_B-x_A\:;\:y_B-y_A\:;\:z_B-z_A)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-02a80d513da6781c07b3950eb8d6d0a2_l3.png)
![Rendered by QuickLaTeX.com \[(x\:;\:y\:;\:z)=(1\:;\:-2\:;\:0)+t\cdot (2-1\:;\:3-(-2)\:;\:-1-0)=(1+t\:;\:-2+5t\:;\:-t)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-07df67589ca5ce6a9849bf55ea2089f9_l3.png)
L’equazione della generica sfera di centro
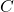
e raggio incognito

è data da
![Rendered by QuickLaTeX.com \[(x-x_C)^2+(y-y_C)^2+(z-z_C)^2=r^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-ac360e12679d56868ffc833c19702cce_l3.png)
![Rendered by QuickLaTeX.com \[(x-1)^2+(y+6)^2+(z-7)^2=r^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-f61b141f7375b6e0d0965ed8aa227063_l3.png)
Una volta determinato questo andremo a risolvere il sistema
![Rendered by QuickLaTeX.com \[\begin{cases} (x\:;\:y\:;\:z)=(1+t\:;\:-2+5t\:;\:-t) \\(x-1)^2+(y+6)^2+(z-7)^2=r^2 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-2b9d8ae0ea32271164af74151311a8d8_l3.png)
cercando il raggio

in maniera tale che il delta dell’equazione di secondo grado che risolve il sistema sia nullo. Pertanto per sostituzione otteniamo
![Rendered by QuickLaTeX.com \[(1+t-1)^2+(-2+5t+6)^2+(-t-7)^2=r^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-96e19f984dab8b86b5ec39a33d46fc11_l3.png)
![Rendered by QuickLaTeX.com \[t^2+16+25t^2+40t+t^2+49+14t-r^2=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-e13909e787f671f28f4869407f4dda9b_l3.png)
![Rendered by QuickLaTeX.com \[27t^2+54t+65-r^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-4db5717de55c4bebce853889717a34c7_l3.png)
da cui
![Rendered by QuickLaTeX.com \[\Delta=54^2-4\cdot 27\cdot (65-r^2)=108r^2-4104\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9ef745cb6f0910c33fa4daa31357116c_l3.png)
e quindi
![Rendered by QuickLaTeX.com \[\Delta=0\Rightarrow 108r^2-4104=0\Rightarrow r^2=38\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6c59c1a1c5b59729d92045ceebe412ad_l3.png)
Pertanto l’equazione della sfera sarà
![Rendered by QuickLaTeX.com \[(x-1)^2+(y+6)^2+(z-7)^2=38\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-b269423f2a019fa62fc8e433be7a3c25_l3.png)
Ritorna all’indice
Quesito 4
Partiamo dalla prima parte del quesito e cerchiamo di capire che caratteristiche hanno i parallelepipedi rettangoli a base quadrata di volume costante 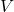 . Se di tale parallelepipedo chiamiamo
. Se di tale parallelepipedo chiamiamo 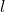 il lato di base e
il lato di base e 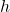 l’altezza possiamo senza dubbio dire che
l’altezza possiamo senza dubbio dire che
![Rendered by QuickLaTeX.com \[A=2l^2+4lh\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-354477b5a83e9fedead6e6877fcde8c4_l3.png)
![Rendered by QuickLaTeX.com \[V=l^2h\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-330fdfcabb5c17e5920a1bfe4e9a9f60_l3.png)
da cui
![Rendered by QuickLaTeX.com \[h={V\over l^2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d65354c1a776671da3729649e22ed459_l3.png)
![Rendered by QuickLaTeX.com \[A=2l^2+4l\cdot {V\over l^2}=2l^2+{4V\over l}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-89e8b54edb0586bd990d35819f5e2824_l3.png)
Una volta determinata l’espressione analitica dell’area totale che dipende dall’unico parametro
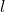
è possibile minimizzare la funzione e determinare che caratteristiche deve avere
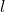
per far si che l’area totale sia la minima possibile. Quindi partiamo da
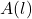
e calcoliamo la sua derivata prima rispetto a
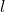
, ossia
![Rendered by QuickLaTeX.com \[A'(l)=4l-{4V\over l^2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-ef1de1ce58abf23e059dcef8ff542da0_l3.png)
da cui
![Rendered by QuickLaTeX.com \[A'(l)=0\iff 4l-{4V\over l^2}=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-3edfb35939454ab4669638bc2f1150b6_l3.png)
![Rendered by QuickLaTeX.com \[4l={4V\over l^2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-e34488e95a1ee286d79bee6eb0757e80_l3.png)
![Rendered by QuickLaTeX.com \[l^3=V\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-0b487be679b6990be807ac54496e4378_l3.png)
![Rendered by QuickLaTeX.com \[l=\sqrt[3]{V}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d8d2dc2cd3e3ab2ded77175b655aa966_l3.png)
e studiando il segno della derivata prima possiamo dedurre che questo è un punto di minimo della nostra funzione
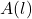
. Per completare il quesito ci basta verificare quale sia la condizione di lunghezza minima della diagonale. Sappiamo che
![Rendered by QuickLaTeX.com \[d=\sqrt{l^2+l^2+h^2}=\sqrt{2l^2+{V^2\over l^4}}=\Big(2l^2+{V^2\over l^4}\Big)^{1\over 2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-32094ed8d0b388a7b40b5f41a6f91de9_l3.png)
per cui la derivata della funzione
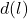
sarà
![Rendered by QuickLaTeX.com \[d'(l)={1\over 2}\cdot \Big(2l^2+V^2l^{-4}\Big)^{-{1\over 2}}\cdot \Big(4l+{(-4)V^2\over l^5}\Big)={2l-{2V^2\over l^5}\over \sqrt{2l^2+{V^2\over l^4}}}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-380b85650f95f2f03948f201ebc992e7_l3.png)
da cui, considerando che il denominatore è sempre maggiore di zero, avremo che
![Rendered by QuickLaTeX.com \[d'(l)=0\iff 2l-{2V^2\over l^5}=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-1ce4dfeafae1e60539fdc24c19a2d02e_l3.png)
![Rendered by QuickLaTeX.com \[2l={2V^2\over l^5}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-5ae3b0166376c87a5fc7e05562663668_l3.png)
![Rendered by QuickLaTeX.com \[l^6=V^2\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6ba719fa1cb1bba15f3d1413be828c4c_l3.png)
![Rendered by QuickLaTeX.com \[l=\sqrt[3]V\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-3fb281b7ee032fa0e367b6ddc4c08c6c_l3.png)
Quindi la condizione che rende minima l’area totale è la stessa che rende minima la diagonale.
Ritorna all’indice
Quesito 5
Come due metodi proponiamo quello con il calcolo della derivata e quello che impone che l’intersezione tra retta e curva abbiamo un’unica soluzione doppia. La curva definita dalla funzione
![Rendered by QuickLaTeX.com \[y=\sqrt{25-x^2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-294328a3bcc4096367cca1537f7b05ed_l3.png)
è la semicirconferenza di centro
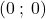
e raggio
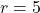
, inoltre passa dal punto
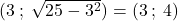
. Una volta dedotto questo partiamo con il primo metodo.
![Rendered by QuickLaTeX.com \[y'={-x\over \sqrt{25-x^2}}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-cc773b716fab99a017b588c42a953e74_l3.png)
per cui

. Quindi la retta tangente alla curva è l’unica retta passante per
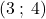
e avente coefficiente angolare
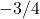
, ossia
![Rendered by QuickLaTeX.com \[y-4=-{3\over 4}\cdot (x-3)\Rightarrow y=-{3\over 4}x+{25\over 4}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-3901072f857afb3d87f6ec4f17c4f3f3_l3.png)
Il secondo metodo è quello studiato in terza che utilizza le conoscenze di geometria analitica. Quindi prima di tutto intersechiamo la generica retta passante per
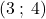
con la circonferenza, ossia
![Rendered by QuickLaTeX.com \[\begin{cases} x^2+y^2=25 \\y-4=m\cdot (x-3) \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-b4dbbb2005591f7fe16bd9877ee28ad6_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2+y^2=25 \\y=mx -3m+4 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-76271b06d4da1662e3e2149879d081f7_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2+(mx -3m+4)^2=25 \\y=mx -3m+4 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-fa77e825150973be38eeec282a5cb5fb_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2+m^2x^2+9m^2+16-6m^2x+8mx-24m-25=0 \\y=mx -3m+4 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-091642bec6319607e679a1ef8e574c92_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} (1+m^2)x^2+(8m-6m^2)x+(9m^2-24m-9)=0 \\y=mx -3m+4 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-46a349d761c5a59cf6011a910ca8ab57_l3.png)
a questo punto determiniamo
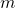
in maniera tale che il sistema abbia un’unica soluzione, ossia che
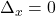
, allora
![Rendered by QuickLaTeX.com \[\Delta_x =0\iff (8m-6m^2)^2-4\cdot(1+m^2)\cdot(9m^2-24m-9)=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d06e91bf13d00cdabd094f21a952d017_l3.png)
![Rendered by QuickLaTeX.com \[64m^2+36m^4-96m^3-36m^2+96m+36-36m^4+96m^3+36m^2=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-245cd300d3d318071332030fb331360c_l3.png)
![Rendered by QuickLaTeX.com \[64m^2+96m+36=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-f91bf98a548aee7ea9175999bab80f9a_l3.png)
![Rendered by QuickLaTeX.com \[\Delta_m=96^2-4\cdot 64\cdot 36=9216-9216=0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-74ea2faa4b8c6e6966f87adf191f02c2_l3.png)
![Rendered by QuickLaTeX.com \[m_1=m_2={-96\pm 0\over 128}=-{3\over 4}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-aad85b0d7dc6493a1678e749a13ea113_l3.png)
Per cui la retta tangente è la stessa di prima, ossia
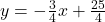 Ritorna all’indice
Ritorna all’indice
Quesito 6
Se proviamo a calcolare
![Rendered by QuickLaTeX.com \[\lim_{x\to 0}{\sin x-(ax^3+bx)\over x^3}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-1f8590b6c11c5bf5c589611d1b297344_l3.png)
ci accorgiamo subito che siamo di fronte a una forma indeterminata del tipo
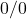
e quindi, viste anche le caratteristiche della funzione, siamo dentro le ipotesi del teorema di de l’Hopital. Per cui
![Rendered by QuickLaTeX.com \[\lim_{x\to 0}{\sin x-(ax^3+bx)\over x^3}=\lim_{x\to 0}{\cos x-(3ax^2+b)\over 3x^2}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-c5c11d3688ba5d397f1caafcaec22d09_l3.png)
questo secondo limite ha il numeratore che tende a
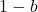
mentre il denominatore tende a
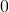
, pertanto se vogliamo che il limite complessivo tendi a
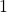
abbiamo come unica soluzione che anche il numeratore tenda a
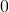
(infatti se sopra ci fosse un qualunque numero diverso da 0 oppure
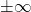
il limite sarebbe
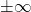
). Da questa osservazione possiamo capire che
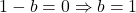
. Una volta determinato questo, per quello che abbiamo già detto, il nostro limite ottenuto tramite de l’Hopital verifica ancora le ipotesi del teorema (per
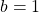
), pertanto
![Rendered by QuickLaTeX.com \[\lim_{x\to 0}{\sin x-(ax^3+x)\over x^3}=\lim_{x\to 0}{\cos x-(3ax^2+1)\over 3x^2}=\lim_{x\to 0}{-\sin x-6ax\over 6x}=-{1\over 6}-a\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-2de2b6e6a0fca3c6ea8089c7526ab2d8_l3.png)
quindi abbiamo
![Rendered by QuickLaTeX.com \[-{1\over 6}-a=1\Rightarrow a=-{7\over 6}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-e9128bd9d996078d539e42d0cdc5e6bc_l3.png)
Ritorna all’indice
Quesito 7
La funzione definita a tratti
![Rendered by QuickLaTeX.com \[f(x)=\begin{cases} -1+\arctan(x) &se\:x<0 \\ax+b &se\:x\ge 0 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-4d5016ac166aa0acfffff7613d8bc586_l3.png)
è una funzione derivabile in ogni suo parte quindi per determinare se è derivabile complessivamente bisogna capire cosa succede per
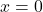
. La funzione derivata
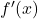
è la funzione
![Rendered by QuickLaTeX.com \[f'(x)=\begin{cases} {1\over 1+x^2} &se\:x<0 \\a &se\:x> 0 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-4bd8cafd98e7872f13c9a0f89ec19460_l3.png)
Per determinare per quali valori di

e
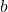
la funzione
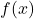
è derivabile prima di tutto determiniamo le condizioni affinchè
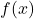
è continua in
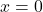
e in seguito quella di derivabilità.
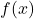
è continua in
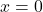
se
![Rendered by QuickLaTeX.com \[\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-25dd0e89ad56b0900aa2d1675cc4db5d_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x\to 0^-}-1+\arctan(x)=\lim_{x\to 0^+}ax+b\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6a3466dc525898474164dae4de2f124a_l3.png)
![Rendered by QuickLaTeX.com \[-1=b\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d57d4b4a2e9e629470ba7746c8f5b366_l3.png)
Una volta determinato
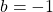
determiniamo la condizione di derivabilità, ossia
![Rendered by QuickLaTeX.com \[\lim_{x\to 0^-}f'(x)=\lim_{x\to 0^+}f'(x)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9859b0fff5344d4d9e7f3757ef8c184a_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x\to 0^-}{1\over 1+x^2} =\lim_{x\to 0^+}a\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-ee4b19880fb7a978616869180837ee6e_l3.png)
![Rendered by QuickLaTeX.com \[1=a\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-aff6a949151f0c3da076968df796e688_l3.png)
Terminiamo l’esercizio rispondendo alla domanda sul teorema di Rolle. Le ipotesi del teorema sono: continuità, derivabilità è l’esistenza di due punti
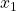
e
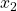
tali che
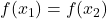
. Abbiamo già provato le prime due condizioni, verifichiamo se è possibile che si verifichi la terza. Osservando la derivata
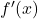
notiamo che questa è sempre strettamente positiva, ne segue che la funzione
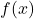
è strettamente crescente e pertanto il teorema di Rolle non può mai verificarsi.
Ritorna all’indice
Quesito 8
La funzione 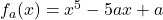 con
con 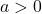 è una funzione continua e derivabile in tutto
è una funzione continua e derivabile in tutto 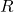 pertanto, dal teorema di Bolzano, possiamo stabilire che
pertanto, dal teorema di Bolzano, possiamo stabilire che 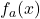 con
con 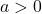 ammette sempre almeno uno zero. Infatti
ammette sempre almeno uno zero. Infatti
![Rendered by QuickLaTeX.com \[lim_{x\to -\infty}f_a(x)=-\infty\:mentre\:lim_{x\to +\infty}f_a(x)=+\infty\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-cacf260121e6bd3032f37e8b8977c043_l3.png)
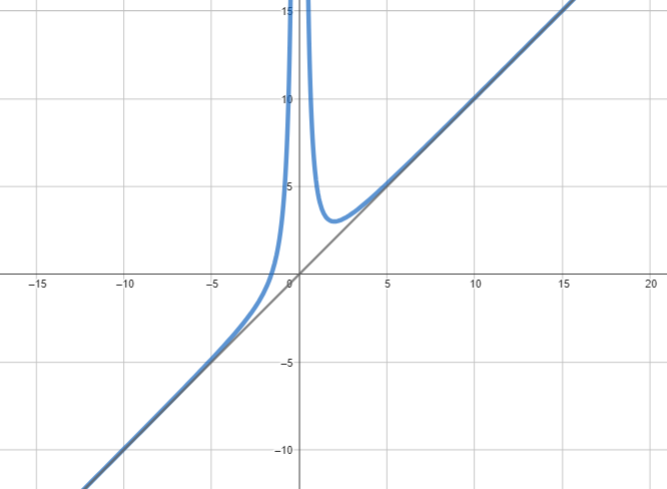
La funzione
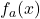
quindi ammetterà tre zeri se partendo da meno infinito passa nella parte positiva delle
poi scende di nuovo nella parte negativa e infine va verso più infinto, insomma se il suo andamento è quello rappresentato da questo grafico
Questa condizione, a livello matematico, può essere espressa dicendo che il massimo relativo della funzione deve essere positivo e il minimo relativo della funzione deve essere negativo, e quindi
![Rendered by QuickLaTeX.com \[f_a^{max}\cdot f_a^{min}<0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-548ea509984c1dc65f226e76f2d73299_l3.png)
Una volta osservato questo andiamo a risolvere l’esercizio. Per prima cosa determiniamo l’espressione del massimo e del minimo relativo sapendo che i due punti annullano la derivata prima, pertanto
![Rendered by QuickLaTeX.com \[f'_a(x)=0\iff 5x^4-5a=0\:con\: a>0\iff x=\pm\sqrt[4]a\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-1c801817b52e46acf142e658adb60f8a_l3.png)
pertanto i punti di massimo e minimo hanno valori
![Rendered by QuickLaTeX.com \[f_a(-\sqrt[4]a)=(-\sqrt[4]a)^5-5a(-\sqrt[4]a)+a=-\sqrt[4]{a^5}+5a\sqrt[4]a+a=a+4\sqrt[4]a\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6c5c04594e5d4d98b5825404fcec3fb5_l3.png)
e analogamente il minimo è
![Rendered by QuickLaTeX.com \[f_a(+\sqrt[4]a)=a-4\sqrt[4]a\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-d67c45db52b520e37081f44e7a20df06_l3.png)
da cui
![Rendered by QuickLaTeX.com \[(a+\sqrt[4]a)\cdot (a-\sqrt[4]a)<0\:con\:a>0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9c11befad02610cedf28ea41bbd22ce7_l3.png)
![Rendered by QuickLaTeX.com \[a^2-16a^2\sqrt a<0\:con\:a>0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-a711fa93faece7d235cc2a04422edb5a_l3.png)
![Rendered by QuickLaTeX.com \[a^2\cdot (1-16\sqrt a)<0\:con\:a>0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-32880f2f22d2ab62d0a7a43e139ec70b_l3.png)
![Rendered by QuickLaTeX.com \[1-16\sqrt a<0\:con\:a>0\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-c498d6ba8e68dd31e2b4434dfe382514_l3.png)
![Rendered by QuickLaTeX.com \[a>{1\over\sqrt {256}}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-eee0634f69e30c9ad847d22c320bba6c_l3.png)
![]() che è
che è ![]()
![]()
![]()
![]() . Sappiamo che il suo dominio è tutto l’insieme dei numeri reali meno lo
. Sappiamo che il suo dominio è tutto l’insieme dei numeri reali meno lo ![]() . Vediamo ora i limiti nei punti estremi del dominio
. Vediamo ora i limiti nei punti estremi del dominio![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , osserviamo anche che tale retta non sarà tangente nel punto
, osserviamo anche che tale retta non sarà tangente nel punto ![]() , ma semplicemente passerà per tale punto. La retta tangente in un generico punto
, ma semplicemente passerà per tale punto. La retta tangente in un generico punto ![]() con
con ![]() ha equazione
ha equazione ![]()
![]()
![]()
![]()
![]() e l’equazione della curva. Risolviamo per sostituzione sostituendo
e l’equazione della curva. Risolviamo per sostituzione sostituendo ![]() e otteniamo
e otteniamo![]()
![]()
![]()
![]() si sposta sempre più a destra
si sposta sempre più a destra![Rendered by QuickLaTeX.com \[\lim_{k\to +\infty}(\int_1^{3\over 2}{x^3+4\over x^2}-(-7x+12)dx+\int_{3\over 2}^k {x^3+4\over x^2}-xdx)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6de9e4f0b1b85781cb7dff30421f17ed_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{k\to +\infty}(\int_1^{3\over 2}8x+{4\over x^2}-12dx+\int_{3\over 2}^k {4\over x^2}dx)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8ffbea42e0f41ff2e7492726923478c8_l3.png)
![]()
![]()
![]() non è derivabile nel punto di ascissa
non è derivabile nel punto di ascissa ![]() calcoliamo il limite del rapporto incrementale da destra e da sinistra e verifichiamo come si comporta. Innanzitutto abbiamo che
calcoliamo il limite del rapporto incrementale da destra e da sinistra e verifichiamo come si comporta. Innanzitutto abbiamo che ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() abbiamo che
abbiamo che![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() e la nostra curva a cuore sono le intersezioni tra le due curve con la retta (infatti nella parte bassa del cuore la curva blu è rappresentata dalla curva
e la nostra curva a cuore sono le intersezioni tra le due curve con la retta (infatti nella parte bassa del cuore la curva blu è rappresentata dalla curva ![]() mentre nella parte alta del cuore la curva rossa è rappresentata dalla curva
mentre nella parte alta del cuore la curva rossa è rappresentata dalla curva ![]() ). Pertanto le coordinate
). Pertanto le coordinate ![]() dei due punti di intersezione sono
dei due punti di intersezione sono ![]() e
e ![]() , osserviamo anche che siccome entrambe le funzioni sono pari a noi basta studiare la situazione per
, osserviamo anche che siccome entrambe le funzioni sono pari a noi basta studiare la situazione per ![]()
![]()
![]()
![]()
![]() è una primitiva di
è una primitiva di ![]() ci basta derivare
ci basta derivare ![]() e vedere che, a meno di una costante, viene
e vedere che, a meno di una costante, viene ![]() . Quindi
. Quindi![]()
![]()
![]()
![]() un triangolo rettangolo isoscele e vediamo che la sua altezza relativa all’ipotenusa deve essere la metà dell’ipotenusa.
un triangolo rettangolo isoscele e vediamo che la sua altezza relativa all’ipotenusa deve essere la metà dell’ipotenusa.
![]() è un angolo di
è un angolo di ![]() , siccome il triangolo grande è un triangolo isoscele e rettangolo, e sicuramente l’angolo
, siccome il triangolo grande è un triangolo isoscele e rettangolo, e sicuramente l’angolo ![]() è un angolo retto siccome
è un angolo retto siccome ![]() è altezza, ne segue che anche l’angolo
è altezza, ne segue che anche l’angolo ![]() è di
è di ![]() e pertanto il triangolo
e pertanto il triangolo ![]() è isoscele. Quindi possiamo concludere che la lunghezza di
è isoscele. Quindi possiamo concludere che la lunghezza di ![]() e la lunghezza di
e la lunghezza di ![]() coincidono, ma sappiamo già che
coincidono, ma sappiamo già che ![]() è la metà di
è la metà di ![]() in quanto nei triangoli isosceli l’altezza relativa alla base è anche mediana.
in quanto nei triangoli isosceli l’altezza relativa alla base è anche mediana.![]() è un triangolo rettangolo tale che l’altezza relativa all’ipotenusa sia esattamente la metà dell’ipotenusa allora
è un triangolo rettangolo tale che l’altezza relativa all’ipotenusa sia esattamente la metà dell’ipotenusa allora ![]() è anche isoscele. Se ci rifacciamo sempre all’immagine di prima abbiamo come ipotesi che
è anche isoscele. Se ci rifacciamo sempre all’immagine di prima abbiamo come ipotesi che ![]() inoltre anche gli angoli
inoltre anche gli angoli ![]() e
e ![]() sono congruenti perchè
sono congruenti perchè ![]() è altezza, ne segue che i due triangoli
è altezza, ne segue che i due triangoli ![]() e
e ![]() sono congruenti e pertanto i due angoli adiacenti all’ipotenusa di
sono congruenti e pertanto i due angoli adiacenti all’ipotenusa di ![]() sono congruenti da cui segue che
sono congruenti da cui segue che ![]() è isoscele.
è isoscele.![]() (ad esempio
(ad esempio ![]() ,
, ![]() ,
, ![]() e così via), pertanto la probabilità di ottenere esattamente due teste è
e così via), pertanto la probabilità di ottenere esattamente due teste è ![]()
![]()

![Rendered by QuickLaTeX.com \[\begin{cases} y={1\over 4}(x+2)^2\qquad &se\:\in [-2\:;\:0] \\ x^2+y^2-1=0\: &se\:\in [0\:;\:1]\\ x^2-y^2-1=0\: &se\:\in [1\:;\:2] \end{cases} \Rightarrow y=f(x)=\begin{cases} {1\over 4}(x+2)^2\qquad &se\:\in [-2\:;\:0] \\\sqrt{1-x^2}\: &se\:\in [0\:;\:1]\\ \sqrt{x^2-1}\: &se\:\in [1\:;\:2] \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8660f97e25bc481afaff9219f3bae5bf_l3.png)
![Rendered by QuickLaTeX.com \[f'(x)=\begin{cases} {1\over 4}\cdot 2\cdot (x+2)={1\over 2}(x+2)\qquad &se\:\in [-2\:;\:0] \\\\{1\over 2}(1-x^2)^{-1/2}\cdot(-2x)={-x\over \sqrt{1-x^2}}\: &se\:\in [0\:;\:1]\\ \\{1\over 2}(x^2-1)^{-1/2}\cdot(2x)={x\over \sqrt{x^2-1}}\: &se\:\in [1\:;\:2] \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-fb79aeb788e9ef96ef24b1b58577c04e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y={x^2-ax\over x^2-a} \\\\y=1 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-0a586ff7031e7d510f311c52062d8969_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y={x^2-ax\over x^2-a} \\y=1 \end{cases}=\begin{cases} 1={x^2-ax\over x^2-a} \\y=1 \end{cases}=\begin{cases} x^2-a=x^2-ax \\y=1 \end{cases}=\begin{cases} -a=-ax \\y=1 \end{cases}=\begin{cases} x=1\\y=1 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9f998607394a92f186299806882a2134_l3.png)
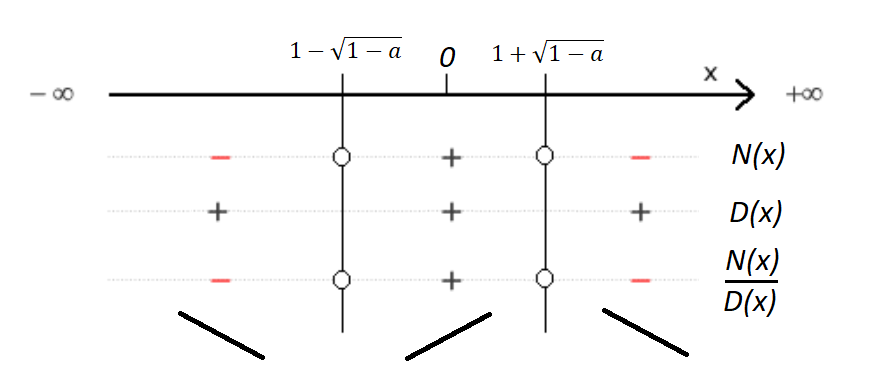
![Rendered by QuickLaTeX.com \[\begin{cases} y={x^2+x\over x^2+1} \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-5a3d996f86c75cff28c2a1ac25a26360_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x={x^2+x\over x^2+1} \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-cc78f07fc5fbb1320a837c4c3a116852_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} (x^2+1)\cdot x=x^2+x \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-1d3a7c020d979c3e5d0be621ed4deb58_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^3+x=x^2+x \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-e83e57e67c9d0464bc22c1e67b3f10fb_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^3-x^2=0 \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-42b2d48e4880b50fb49d1f6df0c32136_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2\cdot (x-1)=0 \\\\y=x \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6b492800f97dcd9e2f610ab2c8ac2c9d_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} p&=2q \\3p+3q&=1 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-9723a37d0a3b74d0ef85be2545e8eced_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} (x\:;\:y\:;\:z)=(1+t\:;\:-2+5t\:;\:-t) \\(x-1)^2+(y+6)^2+(z-7)^2=r^2 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-2b9d8ae0ea32271164af74151311a8d8_l3.png)
![Rendered by QuickLaTeX.com \[d'(l)={1\over 2}\cdot \Big(2l^2+V^2l^{-4}\Big)^{-{1\over 2}}\cdot \Big(4l+{(-4)V^2\over l^5}\Big)={2l-{2V^2\over l^5}\over \sqrt{2l^2+{V^2\over l^4}}}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-380b85650f95f2f03948f201ebc992e7_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2+y^2=25 \\y-4=m\cdot (x-3) \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-b4dbbb2005591f7fe16bd9877ee28ad6_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2+y^2=25 \\y=mx -3m+4 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-76271b06d4da1662e3e2149879d081f7_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2+(mx -3m+4)^2=25 \\y=mx -3m+4 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-fa77e825150973be38eeec282a5cb5fb_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2+m^2x^2+9m^2+16-6m^2x+8mx-24m-25=0 \\y=mx -3m+4 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-091642bec6319607e679a1ef8e574c92_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} (1+m^2)x^2+(8m-6m^2)x+(9m^2-24m-9)=0 \\y=mx -3m+4 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-46a349d761c5a59cf6011a910ca8ab57_l3.png)
![Rendered by QuickLaTeX.com \[f(x)=\begin{cases} -1+\arctan(x) &se\:x<0 \\ax+b &se\:x\ge 0 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-4d5016ac166aa0acfffff7613d8bc586_l3.png)
![Rendered by QuickLaTeX.com \[f'(x)=\begin{cases} {1\over 1+x^2} &se\:x<0 \\a &se\:x> 0 \end{cases}\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-4bd8cafd98e7872f13c9a0f89ec19460_l3.png)