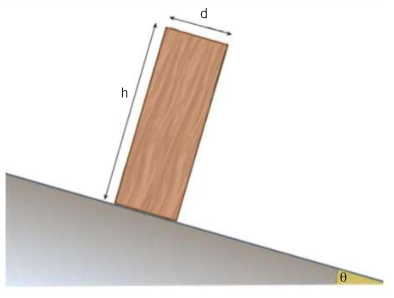
Pietro sta giocando con alcuni blocchi di legno e ne vuole sistemare uno, con lato di base ![]() e altezza
e altezza ![]() su un cuneo, come mostrato nella figura. L’attrito impedisce al blocco di scivolare lungo il piano. Quale è la massima inclinazione
su un cuneo, come mostrato nella figura. L’attrito impedisce al blocco di scivolare lungo il piano. Quale è la massima inclinazione ![]() che può avere il cuneo affinchè il blocco non si ribalti?
che può avere il cuneo affinchè il blocco non si ribalti?
SVOLGIMENTO
Se supponiamo il blocco di legno omogeneo possiamo affermare che il baricentro del blocco si troverà esattamente nel centro del parallelepipedo, a questo punto sappiamo bene che il blocco rimarrà in equilibrio solamente se la proiezione del baricentro cade all’interno della base. La massima pendenza ![]() è quella per cui la proiezione del baricentro cade esattamente sul spigolo in basso a destra del blocchetto, pertanto
è quella per cui la proiezione del baricentro cade esattamente sul spigolo in basso a destra del blocchetto, pertanto
![]()
Per capire il conto tracciamo la proiezione del baricentro e osserviamo che il triangolo rettangolo che si forma ha i cateti di ![]() e
e ![]() mentre l’ipotenusa è il “segmento di proiezione”, per le classiche proprietà dei triangoli simili questo triangolo è simile al blocchetto e pertanto è possibile calcolare l’angolo
mentre l’ipotenusa è il “segmento di proiezione”, per le classiche proprietà dei triangoli simili questo triangolo è simile al blocchetto e pertanto è possibile calcolare l’angolo ![]() del blocco concentrandoci sull’angolo
del blocco concentrandoci sull’angolo ![]() presente in questo triangolino di cui conosciamo i due cateti.
presente in questo triangolino di cui conosciamo i due cateti.
 | TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SULL’EQUILIBRIO DEI SOLIDI |  |