Indice
Problema 1
Per prima cosa calcoliamo la derivata della funzione ![]() che è
che è
![]()
![]()
![]()
Studiamo ora la funzione ![]() . Sappiamo che il suo dominio è tutto l’insieme dei numeri reali meno lo
. Sappiamo che il suo dominio è tutto l’insieme dei numeri reali meno lo ![]() . Vediamo ora i limiti nei punti estremi del dominio
. Vediamo ora i limiti nei punti estremi del dominio
![]()
![]()
![]()
![]()
![]()
![]()
![]()
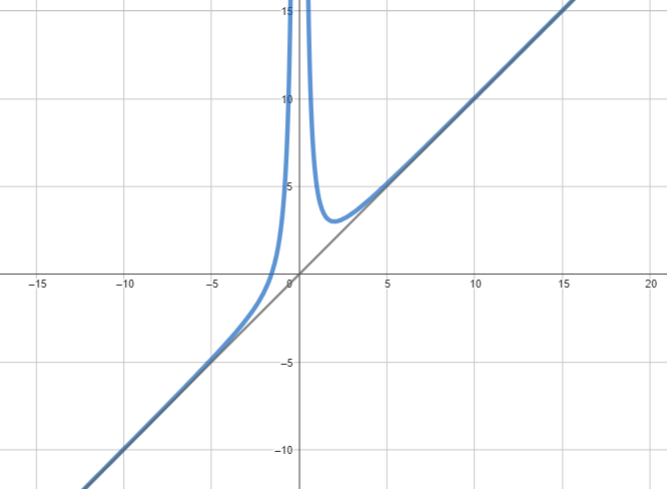
Completiamo ora il punto b) scrivendo l’equazione dell’ulteriore retta tangente alla curva e passante per ![]() , osserviamo anche che tale retta non sarà tangente nel punto
, osserviamo anche che tale retta non sarà tangente nel punto ![]() , ma semplicemente passerà per tale punto. La retta tangente in un generico punto
, ma semplicemente passerà per tale punto. La retta tangente in un generico punto ![]() con
con ![]() ha equazione
ha equazione
![]()
![]()
![]()
![]()
Per risolvere questo punto mettiamo a sistema l’equazione del fascio ![]() e l’equazione della curva. Risolviamo per sostituzione sostituendo
e l’equazione della curva. Risolviamo per sostituzione sostituendo ![]() e otteniamo
e otteniamo
![]()
![]()
![]()
Quello che ci viene chiesto di calcolare è l’area della regione arancione presente in questo grafico man mano che la retta di equazione ![]() si sposta sempre più a destra
si sposta sempre più a destra
geometricamente possiamo subito osservare che tale limite dovrà tendere a un numero proprio per definizione di asintoto obliquo. Vediamo questo dal punto di vista analitico. L’area della figura arancione la possiamo calcolare facendo
![Rendered by QuickLaTeX.com \[\lim_{k\to +\infty}(\int_1^{3\over 2}{x^3+4\over x^2}-(-7x+12)dx+\int_{3\over 2}^k {x^3+4\over x^2}-xdx)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-6de9e4f0b1b85781cb7dff30421f17ed_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{k\to +\infty}(\int_1^{3\over 2}8x+{4\over x^2}-12dx+\int_{3\over 2}^k {4\over x^2}dx)\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-8ffbea42e0f41ff2e7492726923478c8_l3.png)
![]()
![]()
Problema 2
Per verificare che la famiglia di funzioni ![]() non è derivabile nel punto di ascissa
non è derivabile nel punto di ascissa ![]() calcoliamo il limite del rapporto incrementale da destra e da sinistra e verifichiamo come si comporta. Innanzitutto abbiamo che
calcoliamo il limite del rapporto incrementale da destra e da sinistra e verifichiamo come si comporta. Innanzitutto abbiamo che
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Determiniamo ora i parametri

Siccome deve essere simmetrico rispetto all’asse ![]() abbiamo che
abbiamo che
![]()
![]()
![]()
![]()
Ritorna all’indice
Studiamo ora la funzione
![]()
![]()
![]()
![]()
![]()
![]()
![]()

I punti di intersezione tra la retta ![]() e la nostra curva a cuore sono le intersezioni tra le due curve con la retta (infatti nella parte bassa del cuore la curva blu è rappresentata dalla curva
e la nostra curva a cuore sono le intersezioni tra le due curve con la retta (infatti nella parte bassa del cuore la curva blu è rappresentata dalla curva ![]() mentre nella parte alta del cuore la curva rossa è rappresentata dalla curva
mentre nella parte alta del cuore la curva rossa è rappresentata dalla curva ![]() ). Pertanto le coordinate
). Pertanto le coordinate ![]() dei due punti di intersezione sono
dei due punti di intersezione sono ![]() e
e ![]() , osserviamo anche che siccome entrambe le funzioni sono pari a noi basta studiare la situazione per
, osserviamo anche che siccome entrambe le funzioni sono pari a noi basta studiare la situazione per ![]()
![]()
![]()
![]()
Per verificare che ![]() è una primitiva di
è una primitiva di ![]() ci basta derivare
ci basta derivare ![]() e vedere che, a meno di una costante, viene
e vedere che, a meno di una costante, viene ![]() . Quindi
. Quindi
![]()
Infine per calcolare l’area del cuore impostiamo i seguenti integrali
![]()
![]()
Quesito 1
Partiamo con la prima parte della dimostrazione. Sia quindi ![]() un triangolo rettangolo isoscele e vediamo che la sua altezza relativa all’ipotenusa deve essere la metà dell’ipotenusa.
un triangolo rettangolo isoscele e vediamo che la sua altezza relativa all’ipotenusa deve essere la metà dell’ipotenusa.

Sicuramente l’angolo in ![]() è un angolo di
è un angolo di ![]() , siccome il triangolo grande è un triangolo isoscele e rettangolo, e sicuramente l’angolo
, siccome il triangolo grande è un triangolo isoscele e rettangolo, e sicuramente l’angolo ![]() è un angolo retto siccome
è un angolo retto siccome ![]() è altezza, ne segue che anche l’angolo
è altezza, ne segue che anche l’angolo ![]() è di
è di ![]() e pertanto il triangolo
e pertanto il triangolo ![]() è isoscele. Quindi possiamo concludere che la lunghezza di
è isoscele. Quindi possiamo concludere che la lunghezza di ![]() e la lunghezza di
e la lunghezza di ![]() coincidono, ma sappiamo già che
coincidono, ma sappiamo già che ![]() è la metà di
è la metà di ![]() in quanto nei triangoli isosceli l’altezza relativa alla base è anche mediana.
in quanto nei triangoli isosceli l’altezza relativa alla base è anche mediana.
Proviamo ora l’implicazione opposta, ossia ![]() è un triangolo rettangolo tale che l’altezza relativa all’ipotenusa sia esattamente la metà dell’ipotenusa allora
è un triangolo rettangolo tale che l’altezza relativa all’ipotenusa sia esattamente la metà dell’ipotenusa allora ![]() è anche isoscele. Se ci rifacciamo sempre all’immagine di prima abbiamo come ipotesi che
è anche isoscele. Se ci rifacciamo sempre all’immagine di prima abbiamo come ipotesi che ![]() inoltre anche gli angoli
inoltre anche gli angoli ![]() e
e ![]() sono congruenti perchè
sono congruenti perchè ![]() è altezza, ne segue che i due triangoli
è altezza, ne segue che i due triangoli ![]() e
e ![]() sono congruenti e pertanto i due angoli adiacenti all’ipotenusa di
sono congruenti e pertanto i due angoli adiacenti all’ipotenusa di ![]() sono congruenti da cui segue che
sono congruenti da cui segue che ![]() è isoscele.
è isoscele.
Quesito 2
I modi di ottenere esattamente due testa in cinque lanci sono ![]() (ad esempio
(ad esempio ![]() ,
, ![]() ,
, ![]() e così via), pertanto la probabilità di ottenere esattamente due teste è
e così via), pertanto la probabilità di ottenere esattamente due teste è
![]()
![]()
