Indice

• Premessa
• Passare dalla bilancia all’equazione matematica
• Risolvere le bilance più complesse
• Risolvere le equazioni ricorrendo alla bilancia
• Limite dell’utilizzo della bilancia in ambito matematico

Premessa

Un’equazione è un’uguaglianza tra oggetti (matematici contenti una o più incognite), proprio per questo il modo più naturale per introdurre questo concetto è rappresentato dalla bilancia a due piatti. Infatti, se i piatti della bilancia sono in equilibrio, le quantità presenti a destra e a sinistra si equivarranno. Per cui se ci trovassimo di fronte alla seguente bilancia

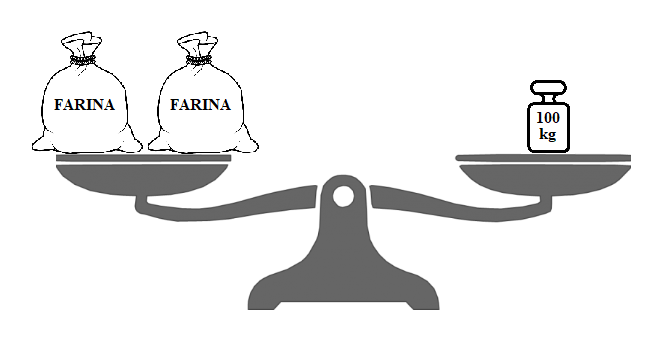
Potremmo concludere che i due sacchi di farina che si trovano nel piatto di sinistra pesano esattamente 100 kg (cioè quello che compare nel piatto di destra) e pertanto un sacco di farina pesa 50 kg.

Passare dalla bilancia all’equazione matematica

Prima di iniziare a risolvere semplici bilance è utile soffermarsi sulle strategie per convertire il linguaggio grafico del disegno in linguaggio simbolico tipico della matematica. Prendiamo come esempio la seguente bilancia

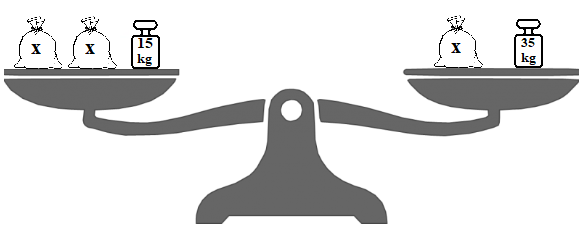
Allora possiamo vedere che nel piatto di sinistra compaiono due sacchi con scritto Più (in italiano potremmo anche dire E) mentre sul piatto di destra compare un sacco con scritto Più (in italiano potremmo anche dire E) . Siccome i due piatti della bilancia sono in equilibrio, e quindi la quantità di sinistra equivale alla quantità di destra, possiamo sicuramente scrivere l’equazione

   

Ricapitolando: sommiamo tutti gli oggetti che compaiono a sinistra, avendo la cura di raggruppare gli oggetti uguali, e li poniamo uguali alla somma di tutti gli oggetti presenti sul piatto di destra.

Esercizi per allenarsi trasformare le bilance in equazioni.

Risolvere le bilance più complesse

Vediamo ora come possiamo risolvere i rompicapo con le bilance. Innanzitutto ricordiamo che risolvere un rompicapo con le bilance vuol dire trovare il valore della che rende uguali i pesi sul piatto destro e sul piatto sinistro. Per fare questo utilizziamo la composizione di due strategia:

• Sottrazione a destra e a sinistra di una stessa quantità
• Divisione a destra e a sinistra di una stessa quantità

Se ci trovassimo di fronte a una bilancia di questo tipo

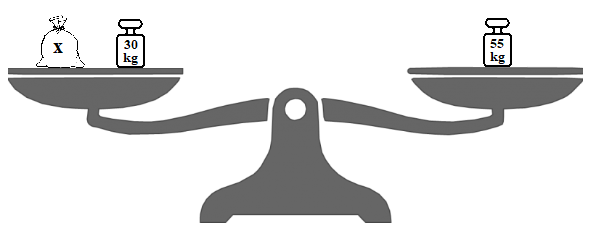
Possiamo osservare che togliendo da entrambi i piatti della bilancia rimarrebbe sul piatto di sinistra solo il sacco con scritto mentre sul piatto di destra . Quindi possiamo certamente dire che il sacco ha un peso di . NOTA che questo lo possiamo dire perché se la bilancia era in equilibrio prima allora avendo tolto la stessa quantità a destra e a sinistra sicuramente rimarrà in equilibrio dopo.

Se invece ci trovassimo di fronte a una bilancia del tipo

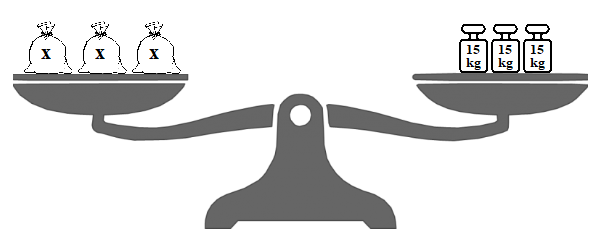
Possiamo osservare che dividendo entrambi i piatti in tre parti uguali otteniamo che ognuna delle parti di sinistra pesa quando una delle parti di destra, per cui il sacco pesa . NOTA che anche questo è possibile da dire perché se la bilancia è in equilibrio prima allora è sicuramente in equilibrio anche dopo.

Vediamo infine come possiamo utilizzare la combinazione di queste due strategie per risolvere le bilance più complesse. Immaginiamo di avere l’esercizio

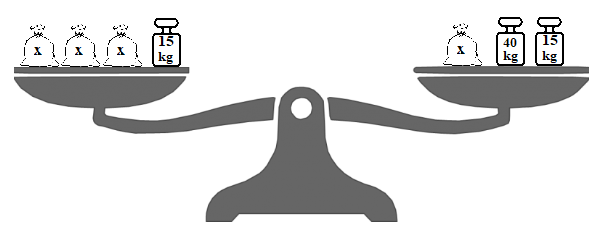
L’obiettivo sarà quello di lasciare tutti i sacchi incogniti sul piatto di sinistra e tutti i pesetti di cui conosciamo il valore sul piatto di destra. Per fare questo dobbiamo ripetere le strategie viste in precedenza quindi per prima cosa togliamo sia a sinistra che a destra ottenendo pertanto la bilancia seguente

Togliendo ora un sacco sia dal piatto di sinistra che dal piatto di destra riesco a separare i sacchi dai pesetti, infatti dopo quel passaggio ottengo la bilancia

Infine, dividendo le quantità presenti su entrambi i piatti in due parti uguali, ottengo in definitiva

dalla quale risulta evidente che un sacco pesa esattamente .

Esercizi per allenarsi a risolvere le bilance.

Risolvere le equazioni ricorrendo alla bilancia

Le bilance ci permettono anche di risolvere semplici equazioni, infatti è possibile trasformare le equazioni scritte in linguaggio simbolico in bilance e poi procedere con le due strategie viste in precedenza. Questo può servire nel periodo iniziale per imparare il meccanismo alla base della risoluzione delle equazioni. Vediamo come possiamo procedere.

Immaginiamo di dover risolvere l’equazione

   

Allora possiamo modellizzare la nostra equazione nella seguente bilancia

E poi risolverla come visto in precedenza. Come primo passaggio togliamo sia dal piatto di sinistra che dal piatto di destra, una volta che tutti i pesetti compaiono solo nel piatto di destra togliamo un sacco sia dal piatto di sinistra che dal piatto di destra e otteniamo che un sacco misura esattamente .

Esercizi per allenarsi a risolvere le equazioni con le bilance.

Limite dell’utilizzo della bilancia in ambito matematico

Prima di terminare l’articolo vogliamo però mettere in guardia il lettore sui limiti dell’utilizzo delle bilance, infatti le bilance presentano almeno due problematiche grandi. La prima è la limitatezza del linguaggio visivo/grafico rispetto al linguaggio simbolico. Per spiegare questo osserviamo che l’espressione

   

pur essendo un’espressione matematica relativamente semplice risulta impossibile da rappresentare con le bilance. NOTA questo problema si potrebbe risolvere semplificando l’espressione prima di risolvere l’equazione con la bilancia, infatti

   

Il secondo limite consiste nell’impossibilità, a meno dell’introduzione di una rappresentazione astratta dei pesetti, di rappresentare i numeri negativi. Ogni volta che le equazioni presentano i numeri negativi o presentano soluzioni negative le bilance non possono venirci in supporto, questo perché nella realtà i pesi negativi non esistono.

In definitiva l’utilizzo delle bilance è estremamente utile nel caso in cui si voglia introdurre il metodo di ragionamento che sta alla base, ma l’obiettivo deve sempre essere quello di passare in un tempo relativamente breve alla notazione matematico simbolica.