La figura mostra il vettore ![]() di modulo
di modulo ![]() e la sua proiezione
e la sua proiezione ![]() sull’asse
sull’asse ![]() .
.
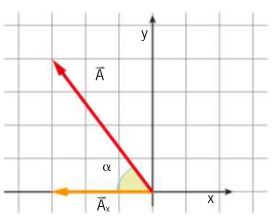
Calcola l’ampiezza dell’angolo ![]() mostrato nella figura.
mostrato nella figura.
Determina la proiezione ![]() del vettore
del vettore ![]() sull’asse
sull’asse ![]() .
.
SVOLGIMENTO
Sappiamo che dato un vettore ![]() e l’angolo
e l’angolo ![]() che il vettore forma con l’asse
che il vettore forma con l’asse ![]() i moduli delle due proiezioni lungo gli assi cartesiani si determinano con le formule
i moduli delle due proiezioni lungo gli assi cartesiani si determinano con le formule
![]()
![]()
Pertanto dalla prima proiezione possiamo determinare l’angolo ![]() per poi inserire tale angolo nella seconda formula e determinare la proiezione lungo l’asse
per poi inserire tale angolo nella seconda formula e determinare la proiezione lungo l’asse ![]() .
.
![]()
Dove osserviamo che nelle formule delle proiezioni l’angolo ![]() è un angolo “orientato” quindi per calcolare
è un angolo “orientato” quindi per calcolare ![]() che è orientato dalla parte opposta devo fare per forza
che è orientato dalla parte opposta devo fare per forza ![]() .
.
![]()
![]()
da cui
![]()
![]()
Osserviamo infine che l’esercizio richiede proprio la proiezione ![]() quindi oltre al modulo bisogna anche aggiungere il versore che caratterizza direzione e verso di tale vettore, cioè
quindi oltre al modulo bisogna anche aggiungere il versore che caratterizza direzione e verso di tale vettore, cioè ![]() .
.
 | TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUI VETTORI E LE FORZE |  |