La figura mostra i vettori 
e 
. I moduli dei due vettori sono 
e 
. Il lato di ogni quadratino vale 
.
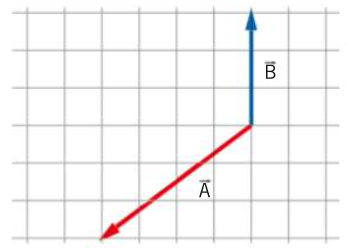
Calcola il modulo di 
. Verso dove è diretto il vettore 
.
SVOLGIMENTO
Per poter calcolare , cioè la componente perpendicolare del vettore rispetto alla direzione del vettore abbiamo la necessità di calcolare l’angolo 
, quindi per prima cosa calcoliamo quell’angolo li.
Per calcolare questo angolo osserviamo che tale angolo è formato da un angolo di 
più l’angolo che il vettore forma con l’asse orizzontale (che chiameremo 
). Tale angolo si può calcolare concentrandoci sul triangolo rettangolo formato dal vettore rosso come ipotenusa e i due cateti di 
e 
quadretti. Pertanto
![\[\tan{\alpha}={3\over 4}\Rightarrow \alpha=\tan^{-1}{3\over 4}\approx 36,9^\circ\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-bd967242c16161b9437467cac8cb5c13_l3.png "Rendered by QuickLaTeX.com")
Da cui
![\[\widehat{AB}=126,9\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-7901c5b5dd9546874a890e11c6bcbff1_l3.png "Rendered by QuickLaTeX.com")
Una volta calcolato questo angolo la componente si calcola facendo
![\[B_\perp=B\cdot \sin{\widehat{AB}}=3\cdot \sin{126,9^\circ}=2,4\]](https://www.brevilezioni.it/wp-content/ql-cache/quicklatex.com-27c3fc5126c49c9ab93ecbf73a4180d2_l3.png "Rendered by QuickLaTeX.com")
Per quanto riguarda invece il verso del prodotto vettoriale ricordiamo che tale verso si può determinare utilizzando la “regola della mano destra”, quindi allineiamo il pollice al vettore e l’indice al vettore e il verso puntato dal dito medio sarà il verso del vettore 
che in questo caso sarà ovviamente perpendicolare ai due vettori e e bucherà il foglio uscendo dalla parte posteriore.
 | TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI SUI VETTORI E LE FORZE |  |
Ma A non è uguale a 5?
Buongiorno, il modulo del vettore A è uguale a 5, ma nel prodotto vettoriale entrano in gioco sia la direzione che il verso quindi non si può utilizzare solamente il 5.